Variation de la focale d’un Schmidt Cassegrain avec sa mise au point
Dans un télescope de Schmidt Cassegrain, la mise au point se fait par déplacement du miroir primaire au moyen d’une vis moletée placée sur barillet arrière du télescope. Cette façon de procéder déplace bien le foyer mais elle a aussi pour conséquence, parfois ignorée, de faire varier la distance focale du télescope dans des proportions significatives.
C’est cette variation de distance focale que nous allons étudier ici. Pour fixer les idées, nous prendrons l’exemple du télescope Célestron C8, de focale 2 000 mm, ouvert à F/D = 10. (F = focale du télescope, D = diamètre du miroir primaire = 200 mm).
Caractéristiques techniques du télescope C8
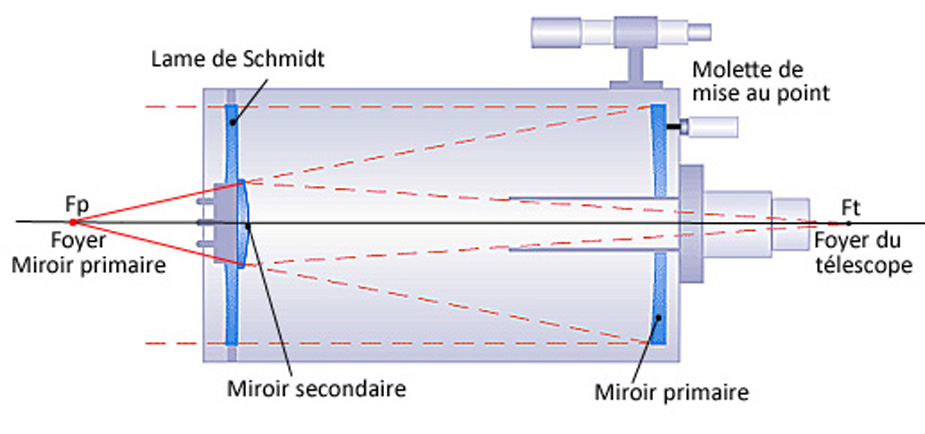 Quand la lumière arrive d’une étoile, elle rencontre successivement :
Quand la lumière arrive d’une étoile, elle rencontre successivement :
- La lame de Schmidt : lame transparente dont le profil (complexe) en épaisseur est ajusté pour compenser l’aberration sphérique du miroir primaire. Bien qu’elle intervienne légèrement sur la distance focale du télescope, nous n’en tiendrons pas compte dans nos calculs.
- Le miroir primaire : c’est un miroir sphérique convergent très ouvert puisque fp/D = 2 (fp = focale du primaire). On en déduit sa focale : fp = 400 mm. Son déplacement assure la mise au point. Il engendre une aberration sphérique qui est corrigée par la lame de Schmidt.
- Le miroir secondaire : collé sur la lame de Schmidt, c’est un miroir hyperbolique divergent ouvert à fs/Ds = 2 (fs = focale du secondaire, Ds = diamètre du secondaire). A ce stade, il faudrait démonter la lame de Schmidt pour mesurer le diamètre du miroir secondaire et en déduire sa focale, ce que je n’ai pas fait.
Par contre, j’ai estimé la distance e = 300 mm entre les deux miroirs et grâce à formule générale des systèmes centrés, il est possible de remonter à fs.
Cette formule s’écrit : 1/F = 1/fp + 1/fs – e/fp.fs (1).
On connaît F = 2 000 mm, fp = 400 mm, e = 300 mm, on en déduit fs = -125 mm, le signe – signifiant que le miroir secondaire est divergent.
Remplacement des miroirs sphériques par des lentilles simples
Le schéma optique d’un instrument composé de plusieurs miroirs est souvent difficile à appréhender. Pour contourner cette difficulté et simplifier notre propos sans nuire à la rigueur, nous allons remplacer les deux miroirs par des lentilles simples.
La lumière provenant d’une étoile rencontrera donc successivement :
- l’objectif d’entrée (noté Lp, de centre optique Op) : lentille convergente de focale fp = 400 mm, dont le déplacement le long de son axe sera chargé d’assurer la mise au point.
- l’objectif de sortie (noté Ls, de centre optique Os) : lentille divergente de focale fs = – 125 mm, fixe, placée à la distance e = 300 mm de l’objectif d’entrée dans sa position initiale (celle qui correspond à la distance focale F = 2 000 mm de l’ensemble).
Quand on visse la molette de mise au point, le primaire s’éloigne du secondaire : l’intervalle e augmente.
Quand on dévisse la molette, le primaire se rapproche du secondaire : l’intervalle e diminue.
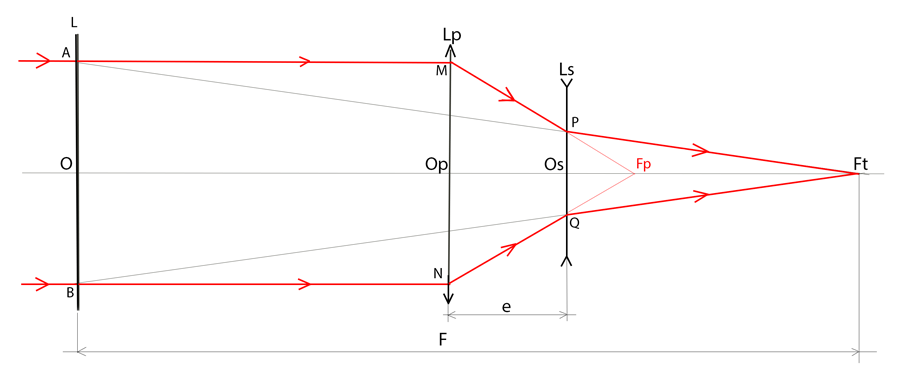
Le schéma optique du télescope avec des lentilles en lieu et place des miroirs est donné ci-dessous. Ce schéma est analogue à celui des téléobjectifs utilisés avec les appareils photo.
 Fonctionnement du télescope
Fonctionnement du télescope
Considérons un faisceau lumineux, matérialisé par les rayons rouges parallèles, provenant d’une étoile située à l’infini. Centrons son image au point focal image Ft du télescope sur le capteur : l’axe optique du télescope OpFt est alors confondu avec la direction du faisceau lumineux.
Les rayons rencontrent d’abord l’objectif convergent Lp (le miroir primaire) aux points M et N. A la sortie de Lp, ils convergent vers le foyer Fp de Lp. Mais avant d’atteindre ce point, ils rencontrent l’objectif divergent Ls (le miroir secondaire) aux points P et Q. Les rayons sortant de Ls sont alors déviés dans l’autre sens et se rencontrent finalement sur l’axe en Ft qui, par définition est le foyer du télescope. C’est dans le plan de Ft perpendiculaire à l’axe qu’on placera le plan du capteur.
Nous avons trouvé la position du foyer du télescope, qu’on peut repérer par la distance OsFt, puisque Ls (miroir secondaire) est fixe durant l’opération de mise au point. Mais OsFt n’est pas la distance focale du télescope.
Pour trouver celle-ci, il faut faire une construction optique à partir des rayons PFt et QFt issus de l’instrument. On les prolonge vers la gauche : ces prolongements viennent rencontrer les rayons incidents provenant de l’étoile aux points A et B.
Par A et B, on trace un trait perpendiculaire à l’axe qui le coupe au point O.
Et quand on regarde la figure obtenue, on remarque que ce trait imaginaire joue le rôle d’une lentille convergente virtuelle qui dévierait les rayons lumineux vers le foyer Ft en absence des objectifs Lp et Ls.
Pour notre propos, le système optique équivalent à l’association des objectifs Lp et Ls séparés de e est donc une lentille convergente virtuelle unique placée en O, de distance focale OFt = F [voir note technique].
Le schéma montre le double rôle de l’objectif divergent Ls (le miroir secondaire) dans l’obtention d’une longue focale avec un instrument (Schmidt Cassegrain ou téléobjectif) de faible encombrement (donné ici par la distance e) :
- Il éloigne vers la droite le foyer Fp de l’objectif Lp (miroir primaire).
- Il reporte loin vers la gauche l’objectif unique équivalent au télescope.
C’est grâce au miroir secondaire qu’on peut avoir OFt bien plus grand que e.
Dans un téléobjectif, la distance e est fixe. La mise au point se fait par déplacement de l’ensemble des lentilles [Lp, Ls].
Dans un Schmidt Cassegrain, la distance e est variable par déplacement du miroir primaire (Lp). On voit tout de suite que ce mouvement déplace bien Ft vers la droite (but recherché), mais déplace aussi la lentille équivalente au télescope vers la gauche, ce qui a pour effet de faire varier la distance focale résultante OFt !!! O et Ft sont translatés en sens contraire sur l’axe optique.
En fait, en translatant le miroir primaire, on change les caractéristiques optiques de l’instrument .
Grâce au schéma optique, nous allons maintenant pouvoir déterminer :
- la variation de distance focale OFt (ou F),
- le déplacement du point focal Ft,
en fonction de la variation de l’intervalle e entre les deux miroirs.
Variation de la distance focale d’un télescope C8 avec le déplacement de son miroir primaire
Le calcul de la focale F se fait facilement avec la formule (1) déjà utilisée :
1/F = 1/fp + 1/fs – e/fp.fs, en faisant varier e, sans modifier les valeurs de fp (400 mm) et fs (-125 mm).
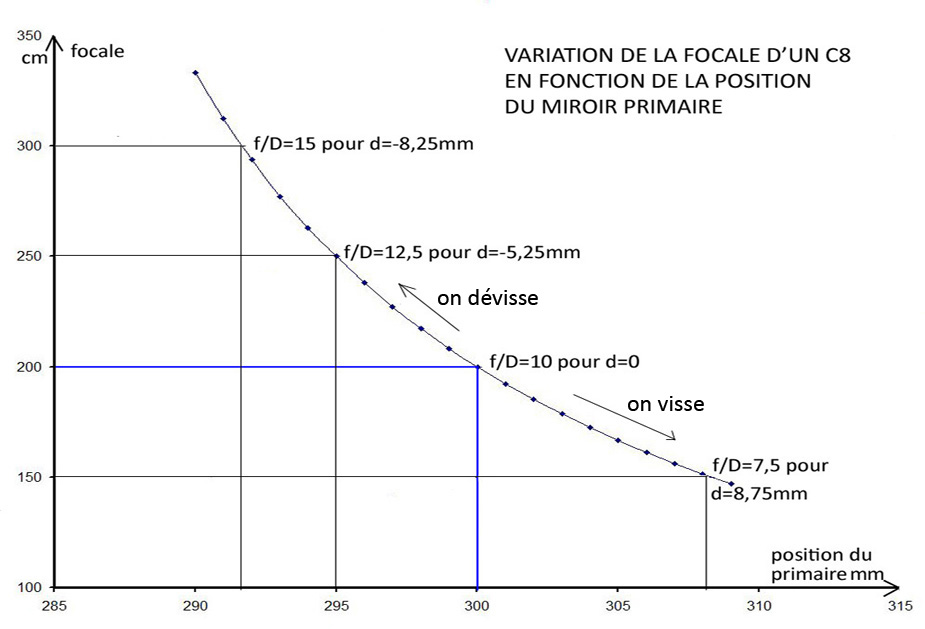
Tous calculs faits, on obtient le graphique 1 suivant :
1) quand on visse la molette, e augmente :
| e(mm) |
300 |
301 |
302 |
303 |
304 |
305 |
306 |
307 |
308 |
309 |
| 1/F(m-1) |
0,50 |
0,52 |
0,54 |
0,56 |
0,58 |
0,60 |
0,62 |
0,64 |
0,66 |
0,68 |
|
F(cm) |
200 |
192,3 |
185,1 |
178,6 |
172,4 |
166,7 |
161,3 |
156,3 |
151,5 |
147,1 |
2) quand on dévisse la molette, e diminue :
| e(mm) |
300 |
299 |
298 |
297 |
296 |
295 |
294 |
293 |
292 |
291 |
| 1/F(m-1) |
0,50 |
0,48 |
0,46 |
0,44 |
0,42 |
0,40 |
0,38 |
0,36 |
0,34 |
0,32 |
|
F(cm) |
200 |
208,3 |
217,4 |
227,2 |
238,1 |
250 |
263,2 |
277,8 |
294,1 |
312,5 |
On constate qu’un déplacement du miroir primaire de quelques millimètres fait varier la distance focale du télescope dans de grandes proportions, par exemple :
– 11% (soit -21 cm) pour un déplacement de +3 mm,
+14% (soit +27 cm) pour un déplacement de –3 mm.
ou encore :
– 20% pour un déplacement de +6mm,
+32% pour un déplacement de – 6mm.
On remarque que cette variation n’est pas linéaire.
Bien évidemment, le nombre d’ouverture F/D du télescope varie dans les mêmes proportions que la focale F.
On diminue l’ouverture F/D à 15 lorsqu’on a dévissé la molette de mise au point de 8,25 mm.
Par contre, on augmente l’ouverture F/D à 7,5 lorsqu’on a vissé la molette de 8,75 mm.
On a déterminé la distance focale du télescope (F), mais on ne connaît ni la position du foyer Ft, ni celle la lentille unique équivalente à l’ensemble (point O) puisque ces deux points se translatent simultanément. Cherchons donc la position du foyer Ft.
Déplacement du foyer du C8 en fonction du déplacement de son miroir primaire
Pour trouver ce déplacement, il faut rattacher la position du foyer Ft à celle de l’objectif Ls (le miroir secondaire) qui reste fixe lors de l’opération de mise au point. Nous allons donc calculer la distance OsFt lorsqu’on fait varier l’intervalle e par déplacement de Lp (le miroir primaire).
Sur le schéma optique, on remarque que le foyer Ft est l’image du foyer Fp de l’objectif Lp à travers la lentille Ls. On va donc utiliser la relation de conjugaison relative à cette transformation qui s’écrit :
1/OsFt = 1/OsFp + 1/fs,
avec fs = -125 mm, et OsFp = OsOp + OpFp = fp – e = 400 – e(mm).
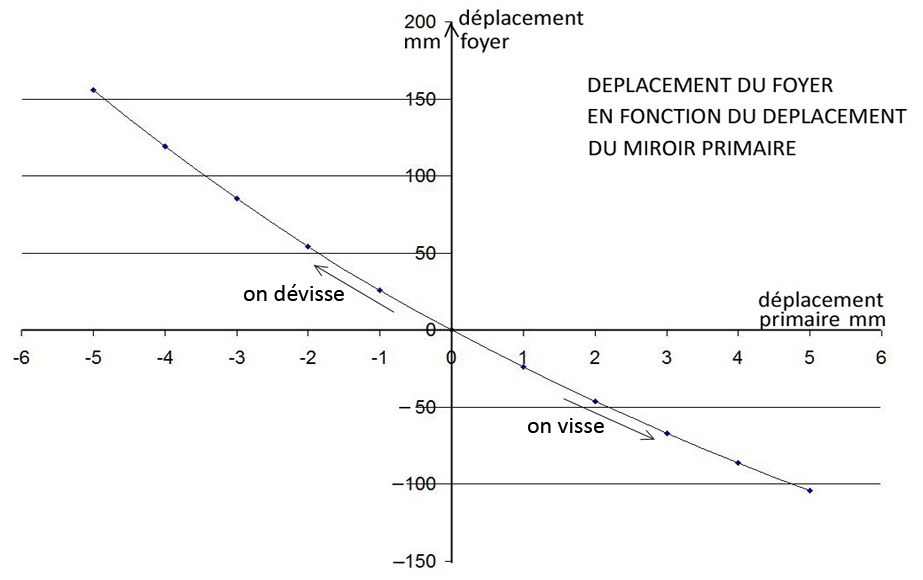
Tous calculs faits, on obtient le graphique 2 ci-dessous :
|
e(mm) |
295 |
296 |
297 |
298 |
299 |
300 |
301 |
302 |
303 |
304 |
305 |
|
dépl. prim (mm) |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
+1 |
+2 |
+3 |
+4 |
+5 |
|
OsFt (mm) |
656 |
619 |
585 |
554 |
526 |
500 |
476 |
453 |
433 |
414 |
396 |
|
dépl.foyer Ft (mm) |
156 |
119 |
85 |
54 |
26 |
0 |
-24 |
-47 |
-67 |
-86 |
-104 |
C’est le déplacement du foyer Ft qui permet de faire la mise au point.
Ainsi, quand on dévisse la molette de mise au point de -3 mm par exemple (e diminue), le foyer Ft recule de 85 mm, et la focale du télescope augmente de 2000 à 2381 mm, c’est-à-dire d’une augmentation bien supérieure au recul du foyer.
Inversement, quand on visse la molette de +3 mm (e augmente), le foyer Ft avance de 67 mm, et la focale du télescope diminue de 2000 à 1667 mm. Là encore, cette diminution de focale est supérieure à l’avancée du foyer.
Conclusion
La « mise au point » du télescope de Schmidt-Cassegrain se fait par une molette qui déplace le miroir primaire par rapport au miroir secondaire fixe.
Cette action provoque un double effet :
- le foyer F du télescope se déplace sur son axe dans le sens opposé à la translation du miroir primaire. Autrement dit, si le miroir primaire avance vers le secondaire (on dévisse, et e diminue), le foyer recule vers l’arrière,
- la distance focale du télescope varie aussi dans le sens opposé à la translation du miroir primaire. Si le miroir primaire avance vers le secondaire (on dévisse, et e diminue), la distance focale augmente.
Quand on dévisse la molette, le foyer Ft recule vers l’arrière et la distance focale F augmente (beaucoup).
Quand on visse la molette, le foyer Ft avance vers l’avant et la distance focale F diminue (beaucoup).
[Note technique] : en réalité, l’association des lentilles Lp et Ls séparés de e n’est pas une lentille simple, mais un « système optique centré » dont nous avons déterminé la position du foyer « image » (Ft) et celle du « Plan Principal Image » (celui passant par le point O). Cette « approximation » simplifie le raisonnement et permet malgré tout de calculer rigoureusement la focale et la position du foyer de l’ensemble. Mais elle ne serait pas utilisable si on s’intéressait au foyer objet du télescope et aux trajets exacts des rayons inclinés…, ce qui nous importe peu ici.
Auteur : Michel Vampouille

Laisser un commentaire