L’image du mois de mai 2010 : rotation d’étoiles autour de la Polaire
Pour l’image du mois de mai, nous restons dans le domaine des filés avec cette rotation classique d’étoiles autour de la polaire. Pourquoi une telle image ?
 Tout d’abord, parce qu’elle est accessible à tout amateur qui possède un APN avec pose B et un simple pied photographique classique sans motorisation.
Tout d’abord, parce qu’elle est accessible à tout amateur qui possède un APN avec pose B et un simple pied photographique classique sans motorisation.
Ensuite parce qu’elle permet de faire des compositions bien sympathiques avec des premiers plans savamment sélectionnés : on en trouve une grande quantité sur Internet, toutes plus jolies les unes que les autres [1].
Enfin, et ce sera notre propos, elle va nous servir de référence pour tenter de calculer le temps que met la Terre pour faire un tour complet de 360° autour de son axe de rotation, c’est-à-dire la durée d’un jour sidéral [2] qui est de 23heures 56minutes 4,09 secondes.
Aura-t-on assez de précision avec le cliché présenté pour affirmer que la durée d’un jour sidéral est différente de celle d’un jour solaire ?
Le temps de pose étant insuffisant, la réponse est négative.
Mais alors, combien de temps doit-on poser pour espérer trouver un résultat avec une erreur absolue de 1 ou 2 minutes ?
Si vous êtes impatient de connaître le résultat, sachez qu’il faut prévoir un temps de pose d’environ 3 heures ! Si le raisonnement vous intéresse, lisez la suite…
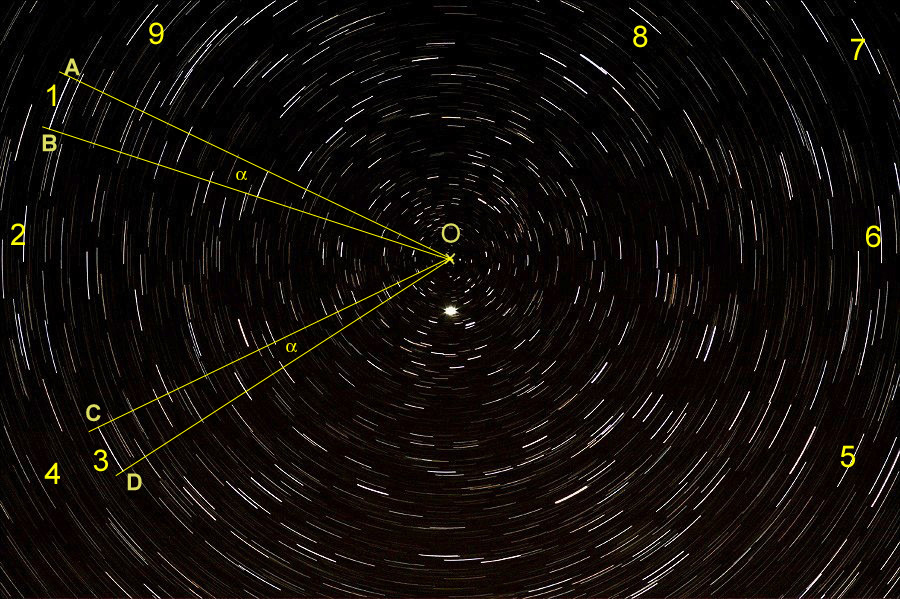
La photographie ci-dessus a été obtenue en mai 2009 par Christophe Mercier à Azerables (23160) avec un APN Canon EOS 40 D équipé d’un objectif Sigma de focale 105 mm ouvert à F/5,6, réglé sur 400 ISO, pointé avec un pied Manfrotto sans motorisation dans la direction de l’étoile polaire. Le temps de pose global est de 30 minutes 5 secondes, correspondant à l’empilement sous IRIS (Starmax convient aussi très bien) de 6 poses de 5 minutes séparées de 1 seconde. En procédant ainsi, on obtient un fond de ciel relativement noir sur lequel les trajectoires circulaires des étoiles se détachent bien.
Pour calculer la durée notée Tjs d’un jour sidéral, nous procédons en 3 étapes :
1) On commence par déterminer le centre de rotation, noté O, de toutes les trajectoires des étoiles. Ceci se fait sur un calque posé sur un agrandissement papier de l’image présentée. Le centre de rotation O est le point de concours des médiatrices [3] tracées avec soin au compas de plusieurs trajectoires circulaires des étoiles les plus éloignées (numérotées pour faciliter leur repérage). On constate, comme prévu, que le point O, replacé sur la photo, ne coïncide pas avec l’étoile polaire (étoile surexposée au centre). Il en est distant actuellement de 40 minutes d’angle environ.
Ensuite, on mesure l’angle au centre, noté α
Cet angle intercepte les arcs de cercle numérotés correspondant à la rotation de la Terre pendant une durée T de 30 min 5 sec (ou 30,083 minutes en notation décimale).
Pour obtenir un maximum de précision, on peut travailler sur une impression d’écran de la partie considérée agrandie au maximum. Un rapporteur d’angles donne une faible précision. Une autre méthode plus précise consiste à mesurer avec soin la longueur des arcs de cercle AB, CD, etc….., et d’en déduire les angles α correspondants par le calcul des sinus des angles moitié avec la relation :
sin (α/2) = AB/2OA [4].
Avec la relation ci-dessus et un agrandissement maximum sur l’écran, nous avons obtenu le tableau de mesures suivant :
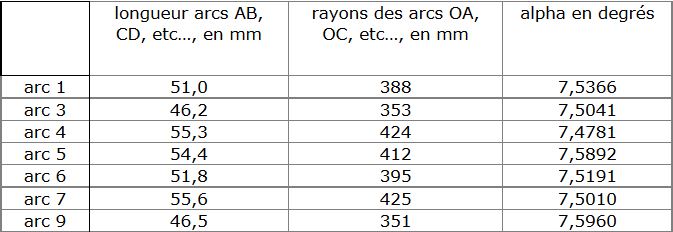 En faisant la moyenne arithmétique des valeurs obtenues, on trouve : α = 7,5320°. Ceci signifie que pendant une durée de 30,083 minutes, la Terre a tourné de cet angle sur elle-même.
En faisant la moyenne arithmétique des valeurs obtenues, on trouve : α = 7,5320°. Ceci signifie que pendant une durée de 30,083 minutes, la Terre a tourné de cet angle sur elle-même.
3) On calcule enfin la durée Tjs d’un jour sidéral : sachant qu’un tour complet correspond à 360°, il est facile de calculer Tjs en minutes avec la relation :
Tjs = 360.T/α = 360×30,083/7,532 = 1437,85 minutes, ou encore : Tjs = 23h 57min 51sec, ce qui est très proche des 23h 56min 4sec escomptées…
4) Quelle est la précision sur cette mesure ?
L’imprécision sur le résultat provient de la mesure des arcs de cercle et de leurs rayons. On peut estimer que les segments AB, CD, etc… sont mesurés sur l’image agrandie avec une erreur absolue de ±0,3mm, alors que les segments font 50 mm en moyenne. Celle des rayons OA, OC, etc… est évaluée à ±1mm sur 400 en moyenne. Ceci nous conduit à une précision (ou erreur relative) de 0,3/50 + 1/400 ≈ 0,8% sur la valeur de α. Celle-ci se retrouve identique sur la valeur de Tjs. L’erreur absolue est donc égale à 0,8.Tjs/100, soit 12 minutes environ. Notre résultat s’écrit donc :
Tjs = 23h 58 min ± 12min, ce qui ne permet pas de différentier la durée d’un jour sidéral de celle d’un jour solaire.
Pour descendre l’erreur à 2 minutes toutes choses égales par ailleurs, il faut la diviser par 6, ce qui revient grosso-modo à multiplier par 6 la longueur des arcs de cercle et donc à prendre un temps de pose 6 fois plus long. Ceci signifie que dans les conditions de notre expérience, il faut poser durant 3 heures au minimum si on veut affirmer, preuve à l’appui, que la différence de durée entre un jour solaire et un jour stellaire est supérieure à 2 minutes. Ceci est à la portée d’un amateur motivé un peu aguerri, mais nous ne l’avons pas encore fait !!!
Pour tout commentaire ou information sur cet article : contact@saplimoges.fr
Références :
[1] http://images.google.fr/images?…..8&source=og&sa=N&hl=fr&tab=wi
[2] http://fr.wikipedia.org/wiki/Jour_sid%C3%A9ral
[3] http://www.mathsgeo.net/rep/dmed.html
[4] http://mathocollege.free.fr/brevet/angles/angles.html
Rédaction : Michel Vampouille

Laisser un commentaire