L’image du mois de février 2021 : un halo parhélique
Ce mois-ci, nous quittons le ciel profond pour le ciel diurne avec une belle image de halo parhélique photographié par Fernanda Baudon le 9 janvier 2021 à 12H 36 depuis les environs de Limoges.
 Cliquer sur l’image pour l’observer en grand format.
Cliquer sur l’image pour l’observer en grand format.
Cette image a été enregistrée avec un Smartphone Samsung S7 modèle SM-G930F, de focale f = 4,2 mm, d’ouverture f/1,7, sur un capteur de dimensions 5,65 X 3,18 mm, possédant des pixels de taille a = 1,4 µm. Le temps de pose est de 1/8 000 seconde à la sensibilité de 40 ISO. Avec un APN de capteur 36 X 24 mm, la focale équivalente serait voisine de 30 mm.
Ce halo parhélique provient d’une double réfraction de la lumière du Soleil dans des cristaux de glace de forme “galette hexagonale” (identiques à de très petits crayons hexagonaux) présents dans les Cirrus et les Cirrostratus qui sont des nuages de l’étage supérieur (5 à 11 km environ). Sa formation est identique à celle des halos paraséléniques qu’on observe en pleine nuit autour de la Lune, voir à ce sujet l’article du mois de janvier 2016.
Si l’atmosphère au niveau du nuage est calme, les cristaux sont tous alignés de manière identique avec leurs faces latérales verticales. La double réfraction sur deux faces latérales non contiguës de chaque cristal produit deux parhélies (aussi appelés faux-soleils), écartés selon un angle Dm de 22/23° de chaque côté du soleil. Pour l’explication de la formation des parhélies, vous pouvez vous reporter à l’article du mois de juin 2015.
Par contre, si l’atmosphère est agitée, les cristaux ne sont plus alignés, ils oscillent dans tous les sens et le phénomène de faux-soleil se répartit sur un anneau circulaire de rayon angulaire Dm = 22/23°, centré sur le soleil : c’est le halo parhélique enregistré ici.
Mesure du rayon angulaire de l’anneau parhélique :
Avec des mesures sur la photo et les caractéristiques techniques (f et a) de l’appareil photo utilisé, on peut calculer le rayon angulaire du halo parhélique sur le capteur :
Le schéma optique du dispositif imageur est le suivant :
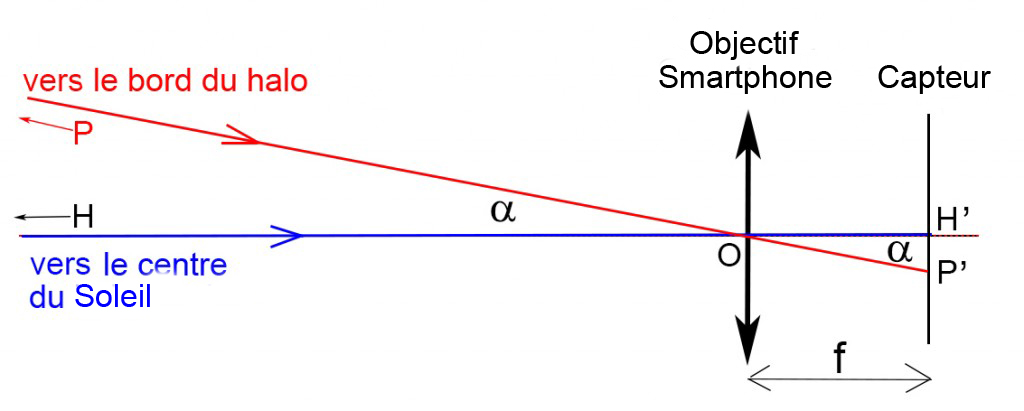
L’objectif Sony du smartphone est simplifié par une lentille mince de centre optique O et de distance focale f = 4,2 mm. On cadre H’, l’image du centre du soleil sur le capteur et aussi du centre du halo, au centre du capteur. L’image du halo entoure le centre H’ ; un des points de ce halo, situé sur un diamètre horizontal est noté P’. Le segment H’P’ sur le capteur représente donc l’image du rayon HP de l’anneau qu’on voit dans le ciel.
Le rayon angulaire de cet anneau est donné par l’angle α (égal à l’angle Dm de l’article de juin 2015 ) qu’on va déterminer à partir de la mesure de H’P’ sur le capteur et de la distance focale f de l’objectif.
Dans le triangle rectangle OH’P’, on a la relation : tan α = H’P’/f.
Le segment H’P’ est mesuré sur le capteur au moyen du logiciel IRIS qui donne les coordonnées en pixels des point H’ et P’. Il vaut : 1290 pixels.
Sachant que la taille du pixel vaut 1,4 µm, on trouve :
H’P’ = 1290 pixels x 1,4 µm = 1 806 µm = 1,806 mm.
Comme f = 4,2 mm, on a : tan α = 1,806/4,2 = 0,43,
d’où on tire α = 23,27°, valeur très proche de celle attendue Dm = 22/23°.
Visibilité du halo parhélique :
La visibilité du halo depuis le sol est liée à l’étendue des nuages dans le ciel qui en sont responsables. Quelle doit être la taille minimum de ces nuages pour qu’un observateur voie l’anneau en entier ?
Pour répondre, il faut déterminer le rayon réel HP du halo qui est localisé dans les nuages supposés être à OH = 10 km au-dessus de l’observateur dans la direction de prise de vue.
Sur le schéma ci dessus, on voit tout de suite que : HP = OH tan α = 10 km x tan (23,27) = 4,3 km.
Ce qui signifie que le volume des nuages (cirrus et cirrostratus) doit s’étendre au moins sur 8,6 km pour qu’on puisse observer un halo depuis le sol. La photo montre que les nuages vont bien au-delà du halo.
Cela signifie aussi que le halo n’est visible qu’à partir d’une zone limitée du sol, définie par la grosseur de tels nuages. Plus les nuages sont étendus, plus la zone de visibilité est étalée.
Coloration de l’anneau :
En bas à gauche de la photo, on distingue une faible couleur rouge à l’intérieur du halo.
Celle-ci est normale et s’explique par la variation de l’indice de réfraction n de la glace en fonction de la longueur d’onde de la lumière solaire qui la traverse, de n = 1,307 pour le rouge à n = 1,317 pour le violet. Cette variation d’indice change légèrement les angles de déviation Dm des rayons sortants doublement réfractés.
Le calcul de ces angles a déjà été expliqué dans l’article de juin 2015. Nous ne le reprenons pas ici.

Laisser un commentaire