L’image du mois de juin 2015 : un parhélie

Cliquer sur l’image pour l’observer en grand format

Pour le mois de juin 2015, nous présentons une image que tout amateur peut réaliser avec un minimum de matériel. Il s’agit d’un gros plan sur un “parhélie” : phénomène atmosphérique relativement courant provoqué par des cristaux de glace plats et hexagonaux contenus dans certains nuages d’altitude, (habituellement, les cirrus). Le parhélie, également appelé “faux soleil”, “soleil double”, ou “sundog”, est un phénomène optique consistant en l’apparition de deux répliques de l’image du soleil, placées horizontalement de part et d’autre de celui-ci et à même hauteur. Ici, on n’en voit qu’une seule, le Soleil étant très loin à droite en dehors de l’image.
Cette photo a été prise par Jean Claude Fayemendy en Charente le 15 décembre 2013 à 16h44 (date et heure importantes pour la suite) au coucher du Soleil avec un APN Canon EOS 70D équipé d’un objectif réglé à la focale de 135mm. Les principales couleurs rouge, jaune et verte de l’arc en ciel (le bleu est difficilement visible) apparaissent nettement sur le faux-soleil se détachant sur le ciel rougeoyant. En cliquant sur l’image pour l’observer avec une résolution supérieure, on distingue même le début du halo parhélique : grand cercle centré sur le Soleil et passant par le 2ème faux-soleil, à droite de celui-ci.

Les différents phénomènes optiques dus à des cristaux de glace ont déjà été évoqués dans l’article du mois de février 2015. Le lecteur intéressé pourra s’y reporter. Pour comprendre la suite, nous retiendrons qu’ici, les cristaux de glace de forme “galettes hexagonales” sont tous orientés parallèles au sol.

IDENTIFICATION CERTAINE DU PHÉNOMÈNE :
Le parhélie est relativement facile à identifier : c’est une double réplique du Soleil située de part et d’autre à 22°, à même hauteur, décomposée en ses différentes couleurs par la  double réfraction sur 2 des 6 faces latérales du cristal.
L’image colorée au centre de l’image avec le rouge du côté du soleil constitue un excellent indice pour prédire un parhélie. Pour être certain à 100%, il faut vérifier que celui-ci se trouve bien à la hauteur du Soleil (que nous n’avons pas sur la photo).
Au moyen de Stellarium, ajusté au bon lieu, à la bonne date et à la bonne heure, il est facile de retrouver la hauteur angulaire du Soleil au dessus de l’horizon : 3° 04′ ou encore 3,07°.
Reste maintenant à mesurer la hauteur angulaire du parhélie sur la photo. Pour cela, nous faisons appel à un petit calcul dont le principe, déjà donné en janvier 2011, est rappelé ici.
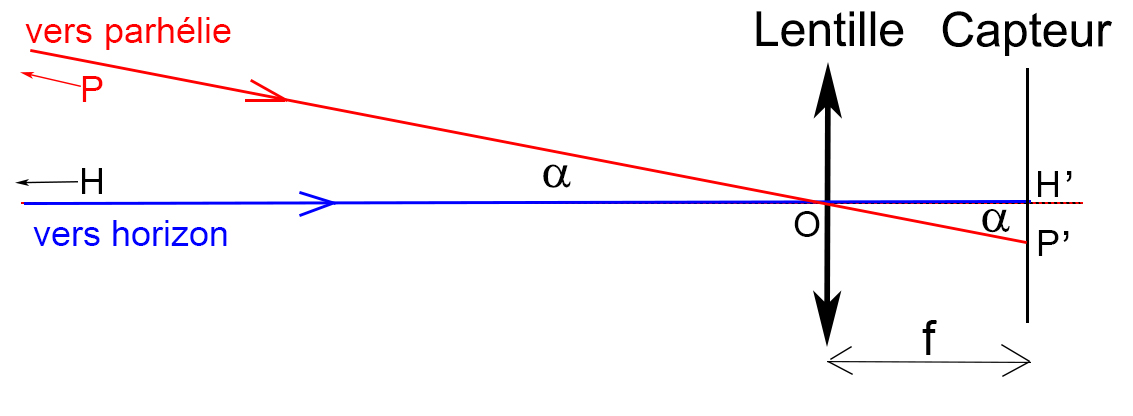Le schéma ci-dessus représente le trajet des rayons lumineux dans l’appareil photo. On simplifie ce schéma en remplaçant le télé-objectif par une lentille simple et on suppose que l’image H’ de l’horizon H (à l’infini) se trouve au milieu de la photo.
Les rayons lumineux provenant du parhélie P à l’infini et passant par le centre optique O de la lentille ne sont pas déviés. L’image du parhélie se retrouve donc en P’ sur le capteur.
On voit tout de suite que la hauteur angulaire du Soleil, notée α, est mesurable à partir des relations trigonométriques dans le triangle OH’P’.
Évaluons la longueur réelle du segment H’P’ sur le capteur :
Sur l’image agrandie, il est facile de constater avec une règle graduée que le segment H’P’ représente 0,48 fois la hauteur totale de la photo. Or, celle-ci est entière ; elle n’a pas été recoupée. D’après le constructeur, la hauteur du capteur est de 15 mm.
Donc, le segment H’P’ mesure réellement : 15 X 0,48 = 7,16 mm.
La distance OH’, c’est la distance focale du téléobjectif, notée f, et égale à 135 mm.
On a donc : tan α  = H’P’/f = 7,16/135 = 0.053,
d’où on tire l’angle α = 3,04°.
Cette valeur est en excellent accord avec celle (3,07°) trouvée sur Stellarium.
Conclusion : l’objet photographié est bien à la même hauteur que le Soleil. C’est un parhélie.

FORMATION DES PARHÉLIES :
L’explication se déroule en 3 étapes :
– calcul de la déviation des rayons solaires après traversée d’un cristal de glace hexagonal
– concentration de l’intensité lumineuse dans certaines directions
– décomposition de la lumière autour de ces directions privilégiées.

1) Calcul de la déviation des rayons solaires :
On suppose que les cristaux de glace de forme “galette hexagonale” sont horizontaux et parallèles au sol terrestre. Leur orientation autour d’un axe vertical est quelconque.
Les parhélies se forment à partir de rayons solaires qui entrent par une des faces latérales du cristal, la face n par exemple, et ressortent après une double réfraction par la face n + 2.
Isolons un des cristaux et dessinons le trajet optique des rayons lumineux.
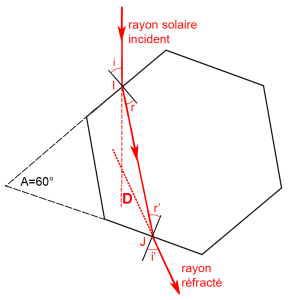Le cristal de glace, de forme hexagonale, est représenté vu de dessus. On s’intéresse aux rayons solaires qui frappent les faces latérales. On a représenté un de ces rayons qui, entrant par la face numéro n au point d’incidence I, va donner un rayon réfracté ressortant par la face numéro (n + 2) au point I’.
Remarquons tout de suite que pour ce rayon, tout se passe comme s’il avait été réfracté par un prisme (amputé) d’angle au sommet A = 60°.
Au point d’entrée I, l’angle d’incidence est quelconque.
Le trajet du rayon lumineux dans le prisme est gouverné par les 4 formules du prisme données ci dessous :
– au point d’incidence I : sin i = n sin r, avec n l’indice de réfraction de la glace,
– au point d’émergence J : sin i’ = n sin r’,
– l’angle au sommet du prisme :  A = r + r’,
– l’angle de déviation D entre le rayon incident et le rayon émergent : D = i + i’ – A.
On remarque que cet angle dépend de l’angle d’incidence i, qui selon l’orientation du cristal, peut prendre toutes les valeurs comprises entre 0 et 90°.
Pour aller plus loin, il nous faut donc calculer numériquement la variation de l’angle de déviation D en fonction de l’angle d’incidence i, sachant que l’indice de réfraction de la glace n vaut 1,3115 pour la couleur verte.
Pour alléger la lecture, nous donnons uniquement les résultats sans les calculs intermédiaires.
On obtient alors le graphique suivant :
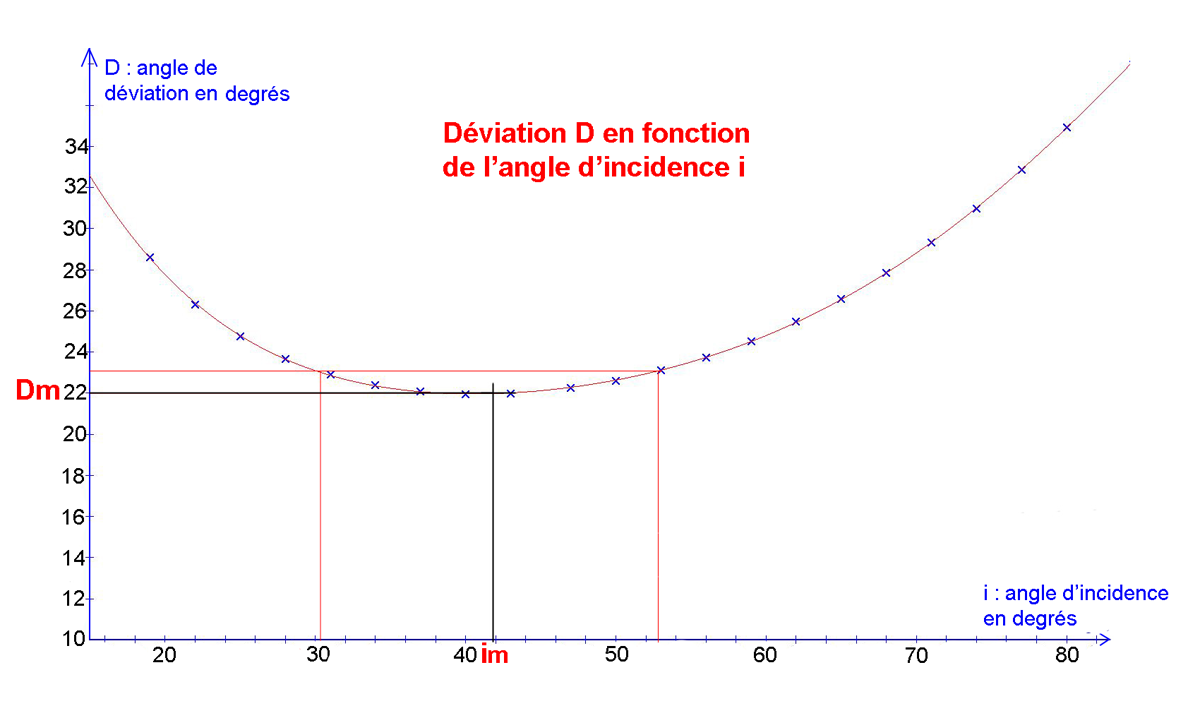L’analyse de cette courbe révèle 2 propriétés importantes qu’on développe dans le paragraphe suivant.

2) Concentration de l’intensité lumineuse dans certaines directions :
On observe tout d’abord que la plage de variation de D ne s’étend que sur 13° [de 22° à 35°], alors celle de l’angle i couvre un domaine de 62° [de 18° à 80°]. Ceci signifie que les rayons sortant des cristaux de glace sont concentrés dans un domaine angulaire restreint. Autrement dit, le parhélie à gauche du Soleil ne peut exister que dans des directions comprises entre 22° et 35° par rapport à celle du Soleil. Dans les autres directions, il n’y a pas de rayons réfractés 2 fois dans le cristal.
Ensuite, on remarque qu’au voisinage du minimum, de coordonnées Dm et im, la courbe est très peu incurvée. Ainsi, lorsque l’angle d’incidence i varie de 30° à 52°, l’angle de déviation conserve une direction pratiquement constante de 22/23°. C’est cette particularité qui est responsable du parhélie.

Expliquons pourquoi en replaçant le cristal de glace dans son environnement au milieu des milliards d’autres qui sont tous éclairés par les rayons solaires provenant  de la même direction.
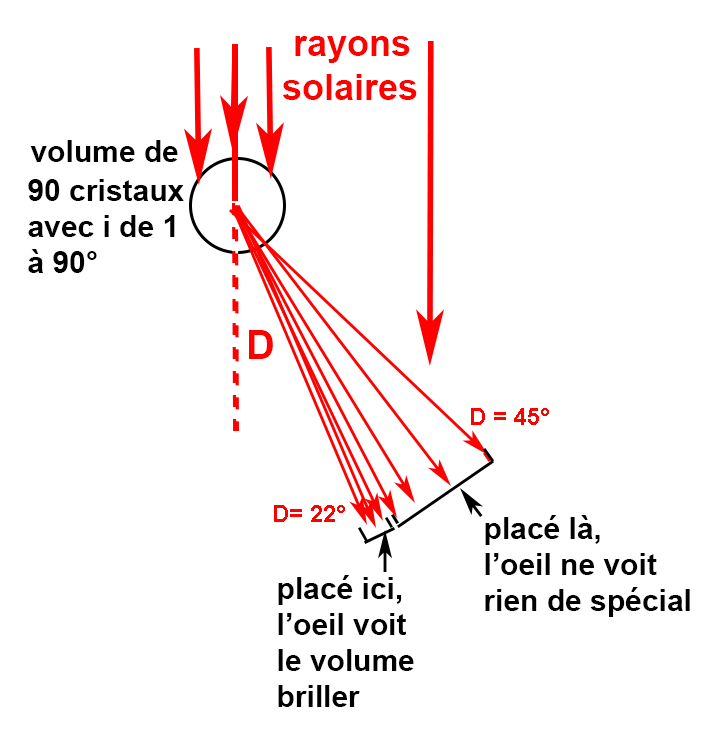Supposons dans le schéma ci-contre que nous puissions isoler un petit volume de nuage contenant 90 cristaux orientés de telle sorte que chaque angle d’incidence diffère de son voisin de 1°. Autrement dit, il y a un cristal avec un angle i = 1°, un autre et un seul avec i = 2°, un autre avec i = 3°, et ainsi de suite jusqu’à 90°.
Comment se répartissent les directions des 90 rayons réfractés par ce petit volume de glace ?
Tout d’abord, les 18 premiers (i de 1 à 18°) ne ressortent pas à la 2ème réfraction (en J). Ils sont emprisonnés dans le cristal et ressortent après une ou deux réflexions internes au cristal. Ils sont donc perdus pour le parhélie.
Il reste les 72 autres qui sont répartis inégalement dans un secteur angulaire compris entre 22° et 45° par rapport à la direction du Soleil. Ils sont très serrés dans la plage [22°-23°] située autour de Dm, 22 exactement, et beaucoup plus espacés ensuite.
Si l’œil d’un 1^er observateur est exactement placé dans la direction Dm = 22/23°, il reçoit un grand nombre de rayons dont l’intensité cumulée devient supérieure à celle issue du nuage lui-même : il voit donc une zone lumineuse de grosseur équivalente ou presque à celle du Soleil : le parhélie.

Un 2^ème observateur, à droite du 1^er (disons 1 ou 2 km), placé en dehors de cette direction, c’est-à-dire dans le secteur angulaire [D = 23 à 45°], reçoit bien quelques rayons provenant du volume éclairé dessiné sur le schéma, mais leur intensité est trop faible pour dépasser celle provenant du nuage environnant : il ne voit rien de spécial dans la direction de ce volume.
Par contre, si le nuage de cristaux est assez grand, et si on suppose (à juste titre) que l’orientation des cristaux est également répartie dans le nuage selon tous les angles d’incidence possibles, il verra un autre volume de cristaux, identique au 1^er, mais translaté à droite dans le ciel de 1 ou 2 km.

Autrement dit, différents observateurs sur Terre, verront un parhélie dans le ciel dans la direction Dm = 22/23° par rapport au Soleil, à condition que dans cette direction, le nuage contienne des cristaux de glace hexagonaux. Ils observent tous des parhélies, mais ceux-ci ne sont pas situés au même endroit dans le nuage. Bien évidemment, le parhélie gauche a son jumeau à 22° à droite du Soleil.

3) Existence d’un spectre coloré autour du parhélie.
Reste maintenant à expliquer pourquoi le parhélie présente plusieurs taches colorées, comme une fraction d’arc en ciel.
La raison vient du fait qu’on a affaire à un phénomène de réfraction et que l’indice de réfraction n de la glace, qui gouverne la valeur de l’angle de déviation minimum Dm, varie très légèrement avec la couleur des rayons lumineux solaires qui traversent le nuage.
La valeur de l’indice n de la glace est donnée dans le tableau suivant :
rouge     orange      jaune      vert       bleu      violet
1,3070   1,3085,    1,3095   1,3115   1,3150   1,3170

La valeur de Dm pour chaque couleur se calcule à partir d’une propriété mathématique des minimums d’une courbe qui, dans notre cas, conduit aux 2 relations suivantes :
Dm = 2 im – A,
sin im = n sin(A/2).
En injectant les différentes valeurs de n pour toutes les couleurs, on obtient :
Couleur : rouge     orange      jaune      vert       bleu      violet
Dm :        21,61°    21,72°      21,80°    21,95°   22,21°   22,34°

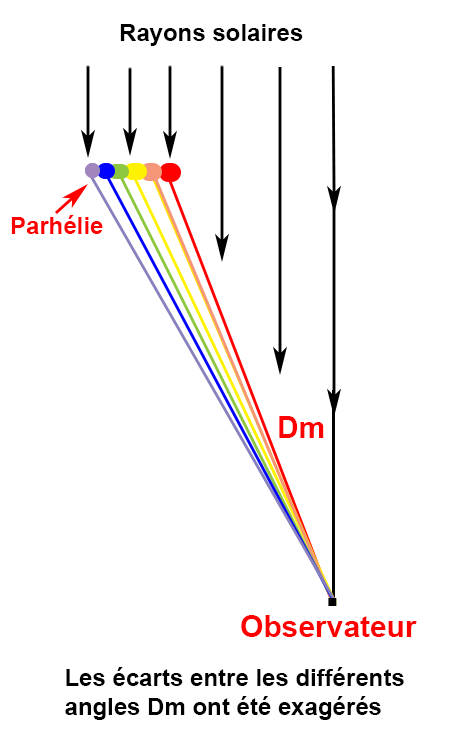
On constate donc que les rayons réfractés rouges sont moins déviés que les jaunes, les verts ou les bleus, ce qui sur un schéma, se traduit par la disposition ci-dessus. Cette disposition est exactement celle qui est photographiée, à ceci près que les zones bleue et violette n’apparaissent pas. Le parhélie ne doit pas être assez intense.

Les parhélies sont relativement fréquents, 1 par semaine environ en Europe…
Il y en a plus en hiver quand le soleil est bas sur l’horizon qu’en été.
Ils deviennent invisibles quand ils sont situés au dessus de 45/50°.

Alors, si ce phénomène atmosphérique vous intéresse : bonne chasse !

Webographie :
http://www.atoptics.co.uk/halo/crhal.htm

Rédaction : Michel Vampouille