Puis-je mesurer SEUL la circonférence de la Terre selon la méthode d’Eratosthène ?
Aujourd’hui, le ciel est dégagé (enfin !).
Puis-je, sans l’aide d’une autre personne physique, reproduire la méthode d’Eratosthène pour déterminer la circonférence de la Terre en mesurant, à midi solaire, la longueur de l’ombre d’un bâton planté en terre ?
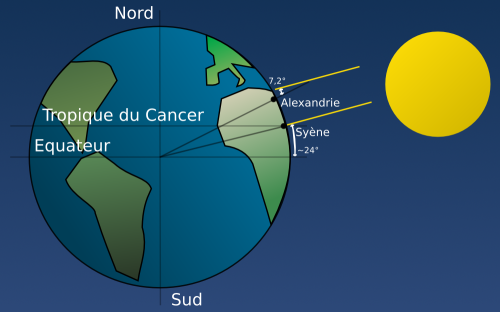
Eratosthène (276-174 avant Jésus Christ), directeur de la Grande Bibliothèque d’Alexandrie, mesure pour la première fois la circonférence de la Terre en remarquant qu’au même instant (au midi solaire), la longueur des ombres d’objets éclairés par le Soleil, à Syène d’une part (Assouan aujourd’hui), et Alexandrie d’autre part, dépend de leur latitude [1], [2], [3]. Appliquant des idées géniales pour l’époque (la Terre est une sphère, le Soleil est très éloigné, les rayons solaires perpendiculaires au sol ne produisent aucune ombre), il trouve que la circonférence de la Terre mesure 40 000 kilomètres, valeur très proche du résultat actuel de 39 941 km.
 Depuis une bonne dizaine d’années, cette méthode constitue une animation pédagogique de premier ordre pour de nombreux clubs, classes ou associations [4], [5]. Cependant, elle nécessite l’accord préalable de deux groupes séparés géographiquement de plusieurs centaines de kilomètres dans le sens Nord/Sud pour réaliser les mesures le même jour au midi solaire, et se communiquer mutuellement les résultats.
Depuis une bonne dizaine d’années, cette méthode constitue une animation pédagogique de premier ordre pour de nombreux clubs, classes ou associations [4], [5]. Cependant, elle nécessite l’accord préalable de deux groupes séparés géographiquement de plusieurs centaines de kilomètres dans le sens Nord/Sud pour réaliser les mesures le même jour au midi solaire, et se communiquer mutuellement les résultats.
Cette nécessité est souvent une excellente source d’échanges fructueux entre deux groupes, mais, a priori, elle ne permet pas de procéder SEUL, à une mesure improvisée débouchant sur un résultat immédiat.
Grâce à Internet et à un ingénieux site [6] qui donne la hauteur du Soleil pour un observateur se trouvant à midi solaire sur le Tropique du Cancer, il est aujourd’hui possible de faire SEUL, en une seule séance, la mesure de la circonférence de la Terre depuis n’importe quel endroit.
La méthode d’Eratosthène nous conduit au schéma suivant :
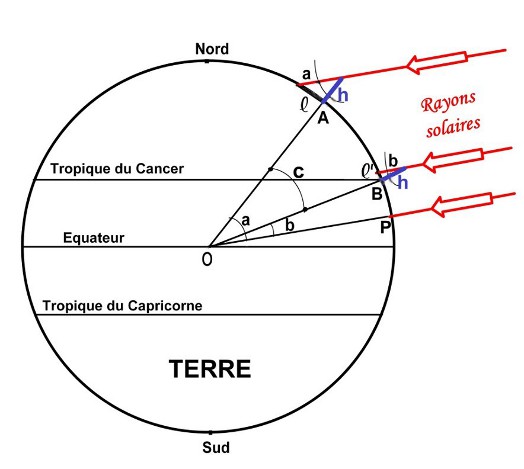 Le jour de la mesure étant quelconque, samedi 4 avril 2009 pour notre exemple, les rayons du soleil au midi solaire sur le méridien du plan de la figure sont perpendiculaires au sol au point P qui est situé n’importe où dans la bande entre l’équateur et le tropique du Cancer. Le 20 juin, jour du solstice d’été, les rayons solaires seraient perpendiculaires au point B, point où la ligne du tropique coupe le méridien.
Le jour de la mesure étant quelconque, samedi 4 avril 2009 pour notre exemple, les rayons du soleil au midi solaire sur le méridien du plan de la figure sont perpendiculaires au sol au point P qui est situé n’importe où dans la bande entre l’équateur et le tropique du Cancer. Le 20 juin, jour du solstice d’été, les rayons solaires seraient perpendiculaires au point B, point où la ligne du tropique coupe le méridien.
L’observateur est au point A, Limoges en l’occurrence. Au midi solaire, il mesure l’angle a que font les rayons solaires avec un gnomon : mot savant pour désigner un bâton de longueur connue h pouvant être orienté perpendiculairement au sol (si on le prolongeait, il rencontrerait le centre O de la Terre). Notre gnomon est constitué par une tige métallique fixée dans un socle de contreplaqué épais sous lequel trois vis calantes permettent de régler l’horizontalité avec un niveau à bulle. Par construction, la tige est perpendiculaire au socle.
Pour trouver l’instant du midi solaire, il suffit de faire des relevés successifs de la longueur de l’ombre du gnomon à partir de 11h30 au soleil (soit 13h30 à la montre) et de repérer la longueur la plus courte. A ce moment, le soleil est au plus haut dans le ciel et la longueur de l’ombre vaut l. Pour déterminer l’angle a, on dispose de deux méthodes selon l’âge des participants : soit on dessine avec précision et à grande échelle le triangle rectangle de côtés h et l et on mesure l’angle avec un rapporteur, soit on passe par la tangente de l’angle qui vaut tan a = l/h, et on en déduit l’angle a avec la fonction inverse sur une calculette.
A ce moment de l’animation, il est bon de faire trouver que l’angle a est aussi celui sous lequel un observateur placé au point O, centre de la Terre, « verrait » l’arc de cercle méridien PA. Les CM2 y sont parvenus sans problème.
Avec notre gnomon de hauteur h = 1 000 mm, nous avons trouvé que le minimum de la longueur de l’ombre, à 13h58 min, mesurait l = 835 mm, ce qui donne un angle d’inclinaison des rayons solaires a = 39,86° (en notation décimale).
Il nous faut maintenant connaître l’angle b, donnant l’inclinaison des rayons solaires par rapport à la verticale au point B se trouvant sur le tropique du Cancer (latitude 23°27′). C’est ici que l’on fait appel au site Internet du collège Antonin Perbosc d’Arras [6], très actif en astronomie ou à celui [7] de l’EEAE (European Association for Astronomy Education). Il suffit de mentionner le jour de la mesure et le lieu : Tropic of Cancer. L’angle b et l’heure du midi solaire s’affichent. Sur le schéma, on constate que l’angle b est aussi celui sous lequel un observateur placé en O verrait l’arc de cercle méridien PB.
Nous avons lu : b = 17,48° à 13h 58 min.
La relation donnant l’angle c est facilement trouvée : c = a – b.
Notre calcul donne : c = 39,86 – 17,48 = 22,38°.
Dernière mesure : la longueur de l’arc AB entre Limoges (le point A) et le point sur le tropique du Cancer situé sur le même méridien que Limoges (le point B). Nous avons réalisé cette mesure sur une carte routière dont on connaît l’échelle. Il faut en trouver une qui contienne Limoges et le tropique du Cancer ! Pour ma part, j’en ai utilisé deux qui se raccordaient au niveau de l’Afrique du Nord. Là encore, les CM2 s’en sont bien sortis.
Plusieurs mesures faites par plusieurs binômes ont conduit à une moyenne : AB = 2447 km.
Dernier calcul : la valeur de la circonférence de la Terre, notée C.
Grâce à un tableau de proportionnalité (qui a détrôné la règle de trois), ou à un petit raisonnement, tout le monde s’accorde pour dire que :
C = AB X (360°/c), soit : 2447 X (360/22,38) = 39 362 km, à comparer à la valeur actuelle de 39941 km (différence : 579 km, soit 1,5%).
Avec les plus grands, on peut faire évaluer les principales sources d’erreurs de mesure :
– la longueur l de l’ombre est imprécise, car la limite de l’ombre n’est pas nette : 5 mm sur 835, donc 5/835 ou 0,6% environ qui se retrouvent grosso-modo sur l’angle a. Celui-ci est donc mesuré à 0,25° près. Cette erreur absolue de 0,25° se transmet sur l’angle c, en admettant que l’angle b est connu exactement. L’erreur relative sur c est donc de 0,25/22,38 =1,1%.
– la distance AB mesurée sur la carte : 5 mm avec une échelle au 1/4.000.000, soit 20 km sur 2447 qui donnent une erreur relative de 1% environ.
– Ces deux erreurs relatives s’ajoutent car elles sont indépendantes. L’incertitude relative sur sur notre résultat est donc de 2,1 % (soit 827 km en erreur absolue), valeur supérieure à notre différence. Ouf !
– Il y a aussi le défaut de perpendicularité du gnomon, mais cette erreur est plus difficile à évaluer.
Si vous travaillez avec soin et méthode, vous serez étonné(e) de la justesse de votre résultat…
Bonnes mesures et bonne chance.
Pour tout commentaire ou demande de renseignement complémentaire : contact@saplimoges.fr
Références :
[1] : http://fr.wikipedia.org/wiki/%C3%89ratosth%C3%A8ne
[2] : La Mesure de la circonférence de la Terre par Eratosthène, Traduction d’un passage du livre de Cléomède « De motu circulari corporum coelestium » – 1 siècle ap JC. version grecque issue du Greek Mathematics édité par Loeb University Press – Classical library -Harvard University Press.
[3] : http://www.lacartoonerie.com/cartoon/id830446499_dessin-anime-eratosthene-arpenteur-terre
[4] : http://lamap.inrp.fr/eratos
[5] : FARGES H, DI FOLCO E, HARTMANN M, Mesurer la Terre est un jeu d’enfant, Paris, Le Pommier, 2002.
[6] : http://perbosc.eratosnoon.free.fr/spip.php?article163
[7] : http://isheyevo.ens-lyon.fr/eaae/groupspace/eratosthene/index_fr

Laisser un commentaire