L’image du mois d’octobre 2016 : aplatissement du Soleil Couchant
Pour le mois d’octobre 2016, avec retard pour des raisons de santé, nous proposons une image banale, mais toujours sympathique, qui rappelle les chaudes journées que nous avons supportées pendant le mois d’août.
Il s’agit d’un coucher de soleil au bord de la mer, mettant en évidence l’aplatissement de celui-ci dû à la réfraction atmosphérique. Cette prise unique a été réalisée à La Tranche sur Mer par la fille de Michel Vampouille le 18 juillet à 22H avec un APN classique Sony de focale 42 mm, à F/13 et 125 ISO, durant 0,001 seconde.

Tout le monde a remarqué qu’à quelques degrés au dessus de l’horizon, le Soleil (et aussi la Pleine Lune) n’apparaissent plus circulaires, mais sensiblement aplatis. Si vous souhaitez connaître la raison de ce phénomène, lisez la suite…
Dans un milieu transparent, la direction des rayons lumineux est gouvernée par l’indice de réfraction de ce milieu. Dans sa définition la plus simple, l’indice de réfraction est un nombre sans unité, souvent noté n, égal au rapport entre la vitesse de la lumière (notée c) dans le vide et la vitesse de phase (notée v) de la lumière dans le milieu, soit n = c/v.
Cette définition simple permet d’observer que l’indice de réfraction dépend par l’intermédiaire de v, à la fois, des caractéristiques du milieu, et de la longueur d’onde (couleur) de la lumière qui le traverse.
Dans un milieu homogène, la lumière se propage en ligne droite. Elle met un temps minimum pour aller d’un point à un autre. C’est le principe de Fermat.
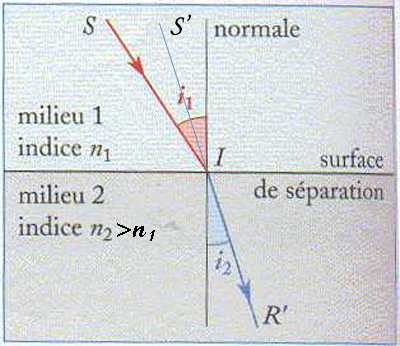 A l’interface de deux milieux d’indice de réfraction n1 et n2, avec n1 < n2, le même critère du temps minimum permet de montrer qu’un rayon lumineux d’angle d’incidence i1 change de direction et ressort avec un angle d’émergence (ou de réfraction) i2 donné par la loi la loi de Snell-Descartes :
A l’interface de deux milieux d’indice de réfraction n1 et n2, avec n1 < n2, le même critère du temps minimum permet de montrer qu’un rayon lumineux d’angle d’incidence i1 change de direction et ressort avec un angle d’émergence (ou de réfraction) i2 donné par la loi la loi de Snell-Descartes :
n1.sini1 = n2.sini2
illustrée par le schéma ci-contre (modifié à partir de [1]).
Si n1 < n2, on voit de suite que l’angle de réfraction i2 est plus petit que l’angle d’incidence i1.
Si S était le Soleil, et R’ l’œil d’un observateur, celui-ci verrait l’image S’ du Soleil dans la direction donnée par l’angle i2. Autrement dit, il observerait le Soleil (son image, en fait) dans une position plus haute que la réalité…!
Revenons maintenant aux rayons solaires traversant l’atmosphère terrestre durant une belle journée d’été sans aucune perturbation. Dans ce cas-là, l’atmosphère terrestre peut être considérée comme un empilement ordonné de couches d’air de plus en plus denses vers les basses altitudes, à cause du poids des couches supérieures qui le compriment. Et comme l’indice de réfraction augmente avec la densité des gaz (supposés ici parfaits), l’atmosphère terrestre présente un indice de réfraction qui varie avec l’altitude. En très haute altitude, l’atmosphère très raréfiée peut être assimilée au vide dont l’indice de réfraction vaut 1. Alors qu’au niveau du sol terrestre, cet indice « monte » à 1,000275. C’est cette toute petite variation continue de l’indice de réfraction qui va provoquer le changement de direction des rayons lumineux, ainsi que l’illustre le schéma ci dessous :
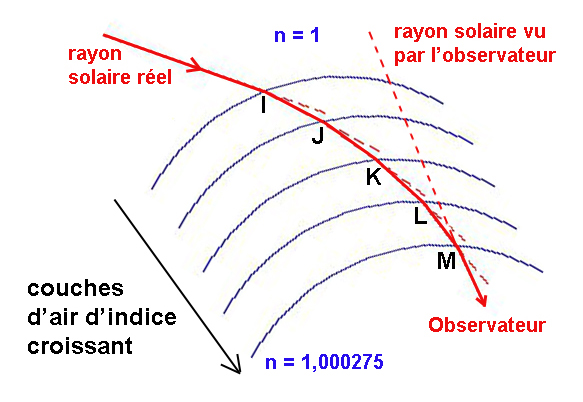
La loi de Snell-Descartes s’applique à chaque interface entre 2 couches. Aux points I, J, K, L, M,…, le rayon lumineux s’incline très légèrement et finalement l’observateur placé sur la Terre voit le Soleil plus haut qu’il n’est en réalité. Pour lui, les rayons lumineux vont en ligne droite en prolongement de la direction selon laquelle il les a reçus (ligne rouge en pointillés).
Il faut donc retenir que, dans des « conditions météorologiques normales », la réfraction atmosphérique courbe les rayons lumineux et remonte la position des astres observés vers le zénith.
Des formules permettent de calculer la courbure en fonction de la direction réelle des rayons solaires, mais aucune n’est valable au voisinage de l’horizon. Les Ephémérides publient une table des angles de réfraction R établies par des mesures très précises (Danjon, Astronomie Générale).
Nous en donnons ici une partie pour souligner quelques résultats qui vont éclairer notre propos. Celle-ci provient du cahier Clairaut 39 [2] où un extrait de la table des Ephémérides est reproduit.
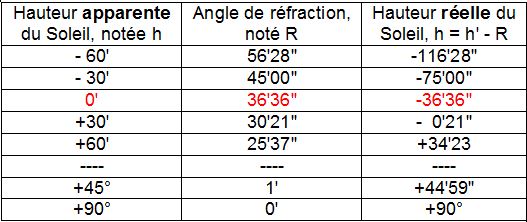 En remontant à partir de la ligne du bas, on remarque successivement que :
En remontant à partir de la ligne du bas, on remarque successivement que :
1) lorsque le Soleil est vu au zénith, il l’est réellement, puisque la réfraction R est nulle.
2) lorsque le Soleil est à 45° au dessus de l’horizon, l’angle de réfraction atmosphérique R ne vaut que 1′, ce qui revient à dire que la position réelle du Soleil coïncide quasiment avec celle observée.
3) la réfraction atmosphérique R ne devient sensible qu’au voisinage des incidences rasantes.
4) lorsque le Soleil est vu sur l’horizon astronomique h = 0′ (plan horizontal au lieu d’observation), il se situe en fait à 36’36 » en dessous de cet horizon, ce qui revient à dire, que si ses rayons se propageaient en ligne droite, on ne le verrait plus !
5) si on monte au sommet d’un phare ou d’une falaise (h’ = -30′, ou -60′), l’angle de réfraction atmosphérique (noté R) augmente par rapport au cas précédent. Autrement dit, plus le Soleil est vu bas, plus l’angle de réfraction augmente.
6) La courbure des rayons du Soleil augmente donc avec sa profondeur sous l’horizon !
Dans la cas de la photo présentée, on obtient le schéma suivant [3] :
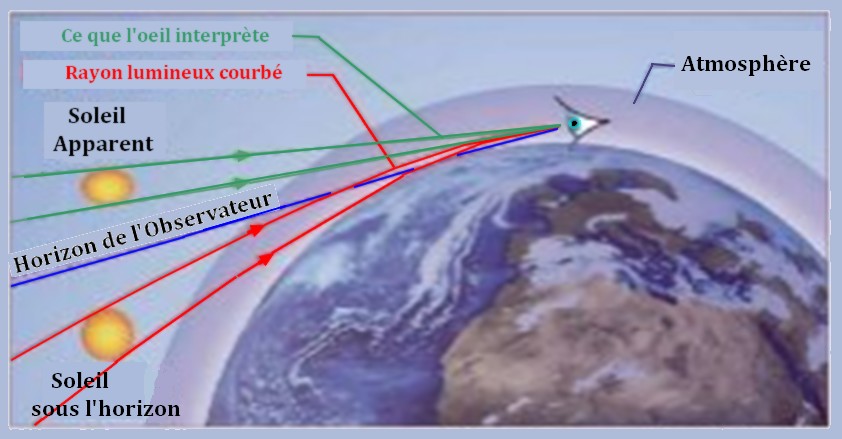 Le Soleil (apparent) observé (obtenu en traçant les rayons tangents (verts) aux rayons courbes (rouges) au niveau de l’œil se situe au dessus de l’horizon astronomique de l’observateur, alors qu’en réalité, du fait de la courbure des rayons lumineux, le Soleil réel a déjà franchi la ligne d’horizon.
Le Soleil (apparent) observé (obtenu en traçant les rayons tangents (verts) aux rayons courbes (rouges) au niveau de l’œil se situe au dessus de l’horizon astronomique de l’observateur, alors qu’en réalité, du fait de la courbure des rayons lumineux, le Soleil réel a déjà franchi la ligne d’horizon.
L’explication de l’aplatissement de l’image du Soleil dans le sens de la hauteur est donnée par les remarques 5 et 6 données ci-dessus.
Vu depuis la Terre, le Soleil présente un diamètre angulaire d’environ 32 minutes d’arc.
 La lumière provenant du bas du Soleil doit donc traverser un air plus dense que celle provenant du haut. DE ce fait, elle est davantage déviée. La partie basse de notre astre se trouve ainsi plus décalée vers le haut relativement à sa partie supérieure, ce qui confère à l’image du Soleil une apparence aplatie.
La lumière provenant du bas du Soleil doit donc traverser un air plus dense que celle provenant du haut. DE ce fait, elle est davantage déviée. La partie basse de notre astre se trouve ainsi plus décalée vers le haut relativement à sa partie supérieure, ce qui confère à l’image du Soleil une apparence aplatie.
Cet aplatissement dépend à la fois de l’altitude de l’observateur, de la position du Soleil par rapport à l’horizon, et des variations atmosphériques de l’atmosphère (un air chauffé est moins dense).
Dans des conditions normales de température et avec un ciel clair, l’aplatissement su Soleil est de l’ordre de 20%. Celui-ci peut atteindre jusqu’à 40%, si l’observateur de trouve au sommet d’une falaise ou d’une petite montagne… [4].
En agrandissant l’image présentée, nous pouvons facilement mesurer ses différentes dimensions.
Avec un diamètre horizontal de 32′ (ne subissant pas de déformation), on trouve un diamètre vertical de 25′, correspondant à un aplatissement de 22%. Dans le sens de la hauteur, l’aplatissement inférieur (28%) est plus prononcé que l’aplatissement supérieur (17%). Ces résultats sont donc conformes aux prévisions.
En conclusion, on retiendra qu’au voisinage de l’horizon, la réfraction atmosphérique nous fait, non seulement apparaître le Soleil plus haut dans le ciel, mais lui confère une forme plus aplatie vers le bas que vers le haut.
Webographie
[1] http://images.google.fr/imgres?imgurl=http%3A%2F%2Fstephane.jean.pagesperso-orange…..
[2] http://acces.ens-lyon.fr/clea/archives/cahiers-clairaut/CLEA_CahiersClairaut_039_09.pdf
[3] http://guy.chaumeton.pagesperso-orange.fr/scphysiques2010/2dph03.htm
[4] https://books.google.fr/books?…..Dictionnaire%20amoureux%20du%20ciel%20et%20des%20%C3
Rédaction : MIchel Vampouille

Laisser un commentaire