L’image du mois d’octobre 2010 ou comment profiter d’une éclipse totale de Lune pour mesurer son rayon
La photographie présentée ce mois fait suite à celle de la Lune éclipsée du mois de juin 2010 [1]. Elle a été enregistrée quelques instants après l’éclipse totale, toujours en digiscopie avec le même APN. La situation particulière de masquage partiel de notre satellite par l’ombre de la Terre ne présente aucun esthétisme particulier, mais par contre, elle permet de réaliser une animation débouchant sur la détermination du rayon de la Lune et de la distance Terre/Lune.
 Au moyen d’un calcul simple, l’exploitation de la photographie prise à ce moment-là nous donne une relation entre le rayon de la Lune et celui de l’ombre de la Terre dans le plan de la Lune. Cette première relation ne suffit pas. Il nous faut aussi utiliser la coïncidence fortuite communément admise par tous les astronomes : depuis la Terre, le Soleil et la Lune sont vus sous des angles apparents quasiment égaux (30′ environ).
Au moyen d’un calcul simple, l’exploitation de la photographie prise à ce moment-là nous donne une relation entre le rayon de la Lune et celui de l’ombre de la Terre dans le plan de la Lune. Cette première relation ne suffit pas. Il nous faut aussi utiliser la coïncidence fortuite communément admise par tous les astronomes : depuis la Terre, le Soleil et la Lune sont vus sous des angles apparents quasiment égaux (30′ environ).
Ensuite, « il n’y a plus qu’à » :
- faire un peu de géométrie plane de niveau 4ème sur un schéma prenant en compte la coïncidence ci-dessus,
- mener le calcul astucieusement en remarquant que le rayon de la Terre est négligeable devant celui du Soleil.
pour démontrer que le rayon de la Lune est égal à celui de la Terre divisé par 3,71. Ce dernier étant connu depuis Eratosthène et mesurable avec l’animation décrite en mai 2010 [2], celui de la Lune s’en déduit facilement.
Notre calcul nous a conduit à un rayon lunaire de 1717 km, valeur très proche des 1738 km admis aujourd’hui.
1ère partie du calcul : exploitation de la photographie de la Lune partiellement masquée :
Après accentuation du contraste de cette photo, sa reproduction sur un calque transparent présente l’allure suivante :
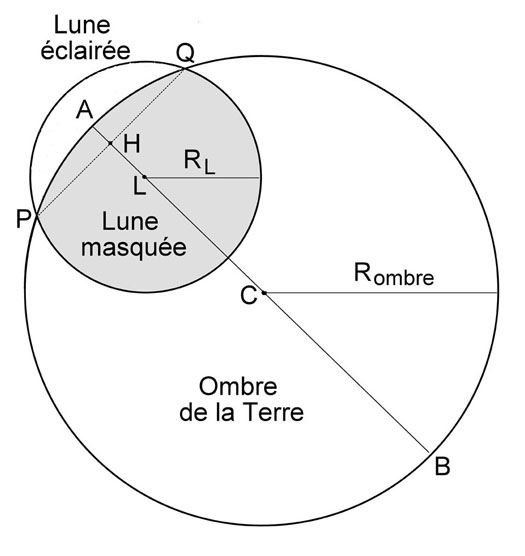
Le disque de l’ombre de la Terre (de centre C, de rayon Rombre) masque partiellement celui de la Lune, de centre L et de rayon RL. Les points d’intersection des deux disques sont P et Q. Sur la médiatrice AB du segment PQ qui le coupe au point H, on trouve les centres C de l’ombre de la Terre et L de la Lune.
Avec un compas et un réglé, il faut déterminer le plus précisément possible :
- la position du centre L de la Lune et son rayon RL,
- la position du centre C de l’ombre de la Terre et son rayon Rombre.
La valeur de RL ne pose pas de difficulté, mais celle de Rombre est plus délicate à obtenir.
On peut la contrôler avec la relation suivante :
HB.HA = HQ.HP = HP2, qui s’écrit aussi : (2Rombre _ HA)HA = HP2, d’où l’on tire facilement :
Rombre = (HP2 + HA2)/2HA.
La mesure de HP et de HA donne alors la valeur de Rombre.
Avec la photo et le raisonnement ci-dessus, nous avons trouvé :
Rombre = 2,71 RL (1).
2ème partie du calcul : exploitation du schéma de l’éclipse à sa totalité
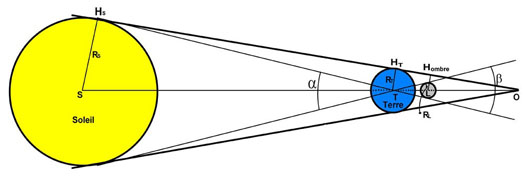
Le schéma reproduit les positions du Soleil, de la Terre et de la Lune au moment de l’éclipse totale en supposant que ces 3 objets sont parfaitement alignés. Cette disposition plus pratique ne change pas la généralité du résultat. Le Soleil (en jaune, centre S, rayon RS), la Terre (en bleu, centre T, rayon RT), la Lune (en gris, centre L, rayon RL) sont placés en respectant l’égalité des angles apparents α et β sous lesquels depuis le centre de T la Terre on voit le Soleil et la Lune. La frontière du cône d’ombre provoqué par la Terre s’obtient en traçant la tangente commune au Soleil (en HS) et à la Terre (en HT). Le prolongement de cette tangente coupe la ligne des centres STL au point O, sommet du cône d’ombre. Le cercle de l’ombre de la Terre est centré en L. A partir de L, on trace la perpendiculaire à la frontière HSO qui la coupe au point Hombre. L’angle du cône d’ombre étant très petit, on peut assimiler le segment LHombre (dessin 2) au rayon Rombre (dessin 1) du disque de l’ombre de la Terre dans le plan de la Lune (non dessiné dans le dessin 2).
On pose donc : LHombre(dessin2) ≈ Rombre(dessin1).
Trois relations nous sont nécessaires pour déterminer RL en fonction de RT :
- Le théorème de Thalès dans les triangles rectangles OSHS, OTHT et OLHombre :
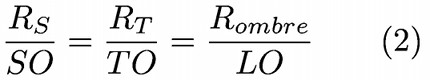
Cette relation peut aussi s’écrire :
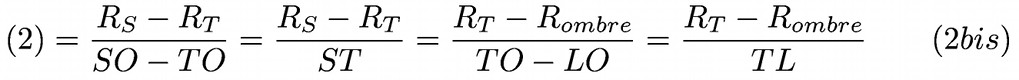
- L’approximation RT << RS :
Cette inégalité permet de négliger RT devant RS dans l’équation (2bis) qui devient :
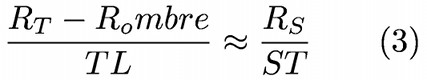
- L’égalité des angles α et β :
En remplaçant les valeurs des (petits) angles α et β en radian par leurs expressions, on obtient :
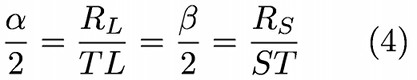
- Le rapprochement des relations (3) et (4) donne le résultat :
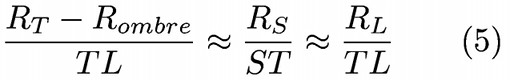
qui conduit à : RT ≈ Rombre + RL.
Il ne reste plus qu’à se souvenir du résultat (1) de la première partie pour aboutir à la valeur cherchée :
RT ≈ 2.71 RL + RL ≈ 3.71 RL, ce qui donne : RL ≈ RT/3.71.Conclusion :
Grâce à la photo prise alors que la lune sortait progressivement du cône d’ombre de la Terre, on peut maintenant estimer que son rayon est approximativement 3.71 fois plus petit que celui de la Terre. - Application numérique :
Dans un article précédent [2], nous avons montré que le rayon de la Terre, mesuré avec l’ombre d’un gnomon selon la méthode d’Ératosthène, valait approximativement : RT = 6 370 km.
Celui de la Lune vaut donc : RL ≈ RT/3.71 = 1 717km.
Quant à sa distance à la Terre, on l’obtient facilement à partir de la relation (4) en prenant la valeur de α égale à 30′ d’angle, soit 0.00870 radian.
On trouve : TL = 2RL / α = 394 700 km.Toutes ces valeurs sont en excellent accord avec celles admises actuellement. Pour tout renseignement complémentaire ou commentaire : contact@saplimoges.fr
- Références :
[1] : L’image du mois de juin 2010.
[2] : Puis-je mesurer SEUL la circonférence de la Terre selon la méthode d’Erathostène ?
Rédaction : Michel Vampouille

Laisser un commentaire