L’image du mois de juillet 2013 : arc circumzénithal

Pour le mois de juillet 2013, voici l’image d’un arc circumzénithal : un phénomène atmosphérique parfois appelé “arc en ciel inversé” dû à des cristaux plats de glace illuminés par les rayons solaires. Cette photographie a été réalisée à Limoges le 05 mai 2013 à 19H 05min par Anthony Hémon, petit-fils de Serge, avec un APN Canon EOS 7D (objectif grand angulaire de 15 mm, ouverture : F/4.5, sensibilité : 320 ISO, temps de pose : 1/2000 sec). Cliquer sur l’image pour l’observer avec une résolution supérieure.

L’arc circumzénithal est un phénomène lumineux qui se forme dans les cristaux de glace plats et hexagonaux (appelés plaquettes) orientés horizontalement, présents dans les cirrus ou les trainées de condensation. Toujours courbé dans la direction opposée au Soleil, il ne dessine généralement qu’un quart de cercle centré au zénith. Contrairement à l’arc en ciel, ses couleurs très pures vont du bleu à l’intérieur au rouge à l’extérieur. L’arc circumzénithal ne peut se former que si la hauteur du Soleil ne dépasse pas 32,2° au-dessus de l’horizon. Toujours très haut dans le ciel, il est le plus brillant lorsque l’altitude solaire est comprise entre 20° et 25° [1] – [2].

L’image de la vignette donnait une idée de la taille du phénomène par référence à celle du nuage. Celle ci-dessus prise avec un objectif de focale 35 mm permet de mieux distinguer les couleurs de l’arc. Cliquer dessus pour l’observer avec une résolution supérieure.

1) Tracé des rayons lumineux dans un cristal de glace :
Dans les nuages d’altitude, les nuages contiennent souvent des cristaux de glace transparents dont la forme peut être assimilée à des cylindres à section hexagonale. Ces cylindres, plats ou épais, tombant vers le sol de manière ordonnée ou non, reçoivent les rayons du soleil, les réfléchissent et les réfractent dans de nombreuses directions qui dessinent dans le ciel une grande variété de motifs caractéristiques.
Dans le schéma ci-dessous expliquant la formation de l’arc circumzénithal, les rayons lumineux entrent par la face supérieure horizontale et sortent par une face latérale après avoir subi deux réfractions dans le prisme d’angle A = 90° formé par cette fraction du cristal de glace.

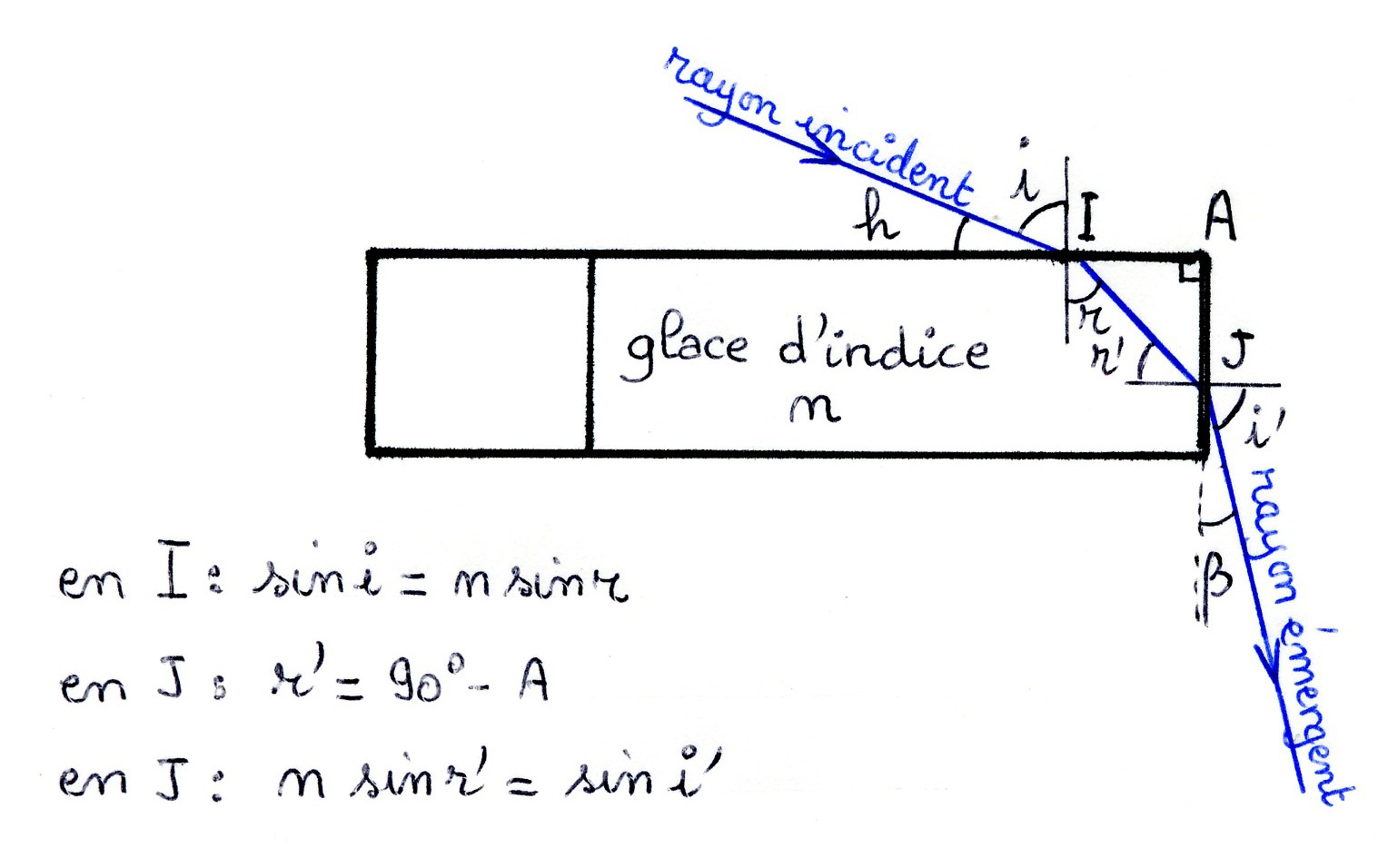1) Un rayon solaire frappe la face supérieure du cristal en I avec un angle d’incidence i, ou une altitude h = 90° – i.
2) Après une première réfraction en I sur la face horizontale, il se propage dans le cristal  avec une direction qui fait un angle r avec la normale à la face.
3) Le lien entre l’angle d’incidence i, l’angle de réfraction r et l’indice de réfraction n de la glace est donné par la relation de Descartes : sin i = n sinr.
4) Ce rayon vient ensuite frapper la face latérale verticale du cristal en J selon une direction qui fait un angle d’incidence r’ et dont la valeur est donnée par : r’ = 90° – r.
5) Il subit alors une 2ème réfraction en J sur cette face et sort du cristal selon une direction qui fait un angle d’émergence i’ avec la normale. Celui-ci est régi à nouveau par la loi de Descartes : n sin r’ = sin i’.
6) Enfin, ce rayon sortant sera vu par un observateur au sol sous un angle β avec la verticale qui est donné par : β = 90° – i’.

2) Indice de réfraction de la glace :
Parmi les nombreux astronomes et physiciens qui se sont intéressés aux figures provoquées dans le ciel par les cristaux de glace, on peut citer Auguste Bravais [3] qui a été le premier à mesurer l’indice de réfraction de ce matériau selon diverses longueurs d’onde avec une erreur absolue de 0,001. Les valeurs qu’il a trouvées sont données dans le tableau ci-dessous :

 rouge     orange      jaune      vert       bleu      violet
1,3070   1,3085,    1,3095   1,3115   1,3150   1,3170

Dans la suite, on prendra n = 1, 3115 comme indice moyen de réfraction de la glace.

3) Conditions d’existence de l’arc circumzénithal :
L’observateur au sol ne verra cet arc que si le rayon IJ frappant la face latérale du cristal en J parvient à sortir (selon l’angle i’). Or ceci n’est pas toujours le cas.
Selon la valeur numérique de l’angle d’incidence r’, il peut arriver que le rayon se propageant dans le cristal se réfléchisse sur la face latérale comme sur un miroir.
A partir de la relation donnée dans (5), on peut prévoir la condition de “réflexion totale” en J. Celle-ci est donnée par : n sin r’ > 1. Dans ce cas, i’ n’existe plus, car le sinus d’un angle ne peut être supérieur à l’unité.
Il y aura donc réflexion en J si : sin r’ > 1/n, soit r’ > 49,68°.
Et donc réfraction avec rayon sortant et formation de l’arc si : r’ < 49,68°.

De relation en relation, on remonte à la condition sur l’angle d’incidence i ou sur la hauteur h du Soleil.
(4) r = 90° – r’> 90 – 49,68 > 40,31°.
(3) sin i > 1,3115 sin 40,31 > 0,849, soit : i > 58,05°
et finalement : h < 90° – 58,05 < 31,95°.
On retrouve bien la valeur indiquée au début : existence d’un arc circumzénithal si la hauteur du Soleil ne dépasse pas 32° au-dessus de l’horizon.

4) Formation d’un arc de cercle centré sur le Zénith :

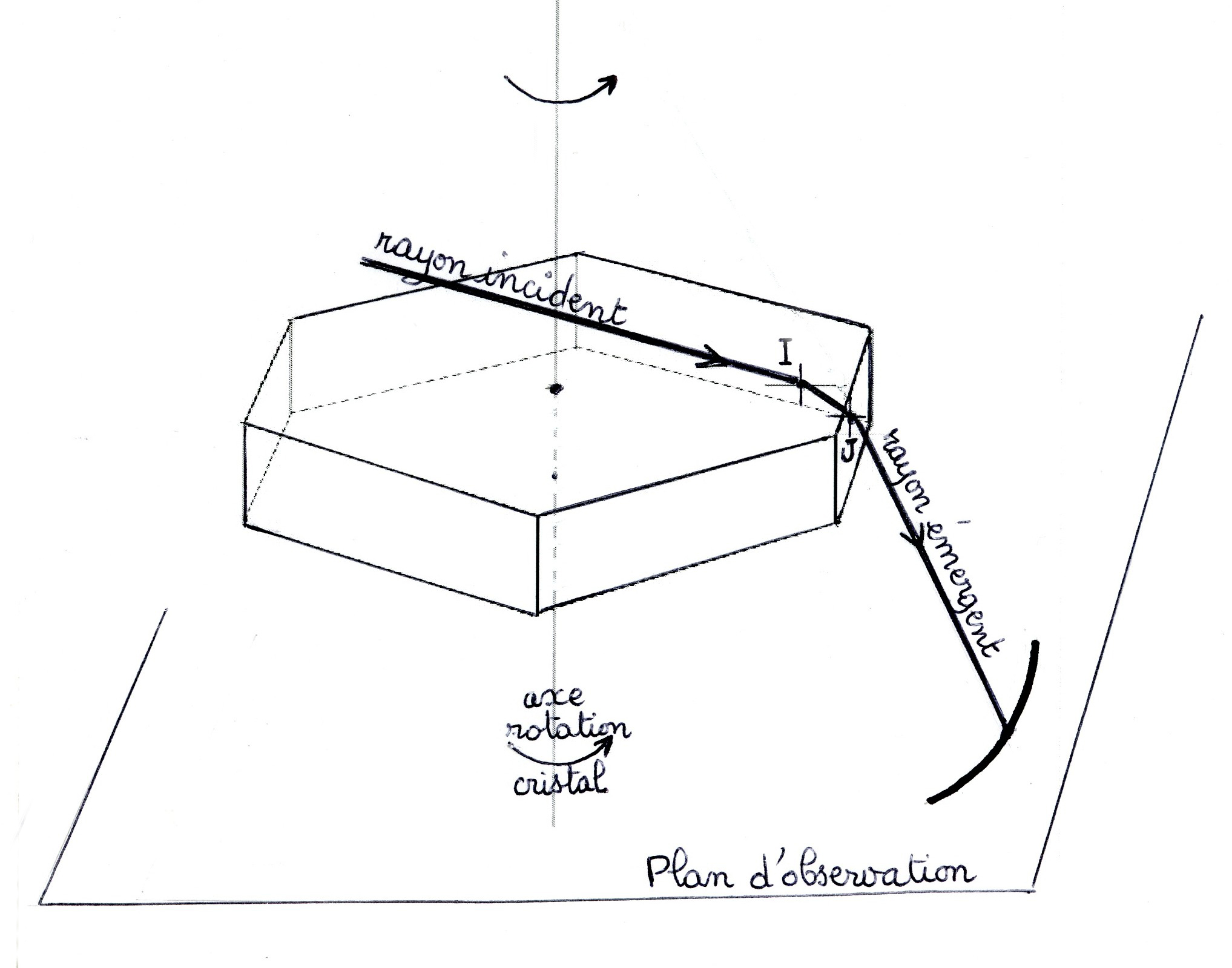4.1) Explication : Jusqu’à présent, nous n’avons considéré que les rayons solaires traversant les cristaux plaquettes dans un plan vertical. Cette situation n’existe qu’avec des cristaux dont une des faces latérales verticales est perpendiculaire au “plan d’incidence” : plan (ici de l’écran) formé par le rayon incident et la perpendiculaire en I à la face supérieure. Or, il n’y a aucune raison physique pour que les cristaux contenus dans le nuage soient tous dans cette position. Ils sont orientés de manière aléatoire et peuvent prendre toutes les orientations possibles, tout en restant horizontaux.
Pour introduire cette notion supplémentaire dans notre raisonnement avec un cristal unique, il faut imaginer que le cristal qui nous sert de modèle tourne sur lui-même autour d’un axe vertical (donc orienté vers le zénith) centré sur ses faces horizontales. Dans ce cas, le phénomène de double réfraction sur les faces horizontale et verticale existe toujours, mais la direction du rayon émergent en J ne reste pas dans le plan d’incidence. Au niveau de la deuxième réfraction en J, le rayon émergent est incliné à la fois dans le sens haut-bas et dans le sens droite-gauche. Autrement dit, il sort de l’écran.
Le calcul est plus délicat, mais on peut quand même prévoir ce qu’il advient au rayon émergent en disant que la figure qu’il dessine dans un plan d’observation horizontal doit satisfaire la condition de symétrie qui a provoqué son changement de direction. Or, la seule figure géométrique qui satisfait la condition de symétrie due à une rotation axiale est un arc de cercle centré autour du même axe. Pour l’observateur situé au sol, un arc de cercle centré sur le zénith se dessinera dans le ciel, chaque point de cet arc correspondant à la position d’un cristal particulier bien orienté dirigeant vers lui son rayon émergent. Les autres cristaux du nuage réfractent aussi les rayons solaires, mais leurs rayons émergents ne pénétrant pas dans l’œil de l’observateur sont ignorés par lui.

4.2) Vérification de la position du centre de l’arc circumzénithal : pour fixer les idées, commençons par montrer les différentes figures dessinées dans le ciel par des cristaux de glace hexagonaux [4].

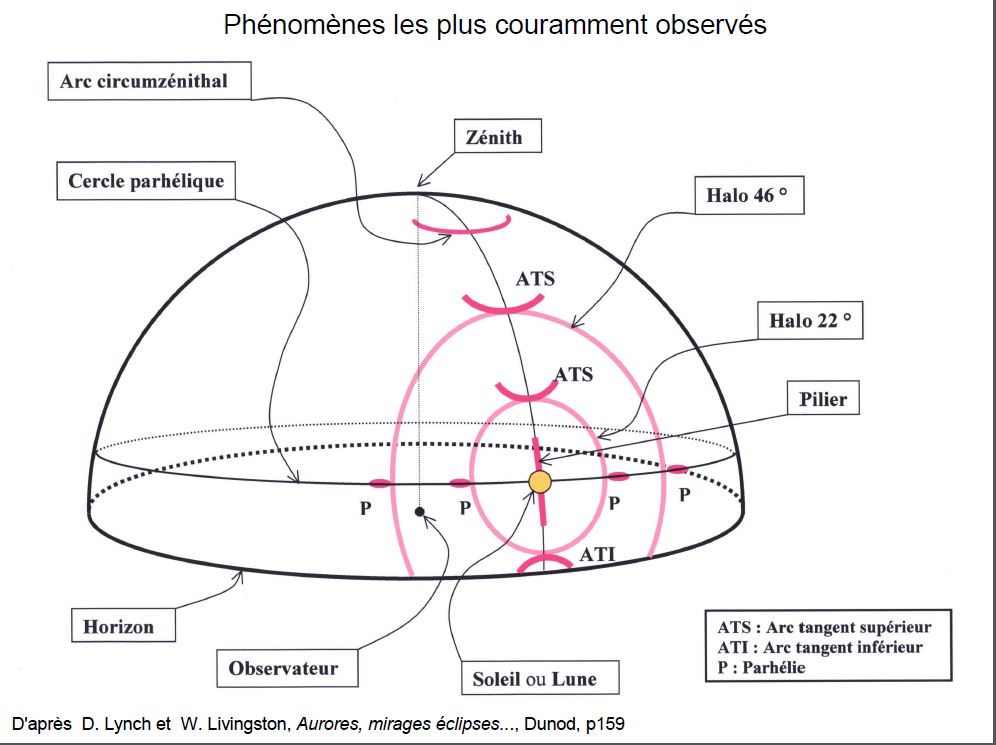Selon la nature (plaquettes ou crayons) et la disposition (aléatoire ou ordonnée) des cristaux de glace, l’observateur placé au centre de la demi-sphère céleste peut voir :
– les parhélies (P) et les halos parhéliques à 22° et 46°,
– les arcs tangents supérieurs (ATS) et inférieurs (ATI),
– le cercle parhélique centré sur le Soleil,
– un pilier solaire,
– et bien sûr, l’arc circumzénithal, qui est une fraction d’un cercle (appelé par le joli nom “d’almi-cantarat”) contenu dans un plan parallèle au plan équatorial.
Tentons, à partir des photos présentées, de vérifier que le centre de ce cercle correspond bien au zénith du lieu.
Pour cela, nous avons besoin de comparer la valeur numérique de deux angles :
– d’une part, l’angle (appelé β = 90 – i’ au paragraphe 1) correspondant à l’inclinaison théorique du rayon sortant avec la verticale du lieu. Celui-ci se calcule de proche en proche avec les relations 1, 3, 4 et 5 déjà citées dans lesquelles on injecte la hauteur h = 19° 36′ du Soleil à Limoges, le 05 mai 2013 à 19H 05min donnée par le logiciel Stellarium convenablement initialisé, et l’indice de réfraction de la glace n = 1,3115 (paragraphe 2). La relation (1) donne l’angle d’incidence i, la relation (3) calcule l’angle de réfraction r, l’angle r’ s’obtient avec (4) : r’ = 90° – r, et la relation (5) conduit à l’angle d’émergence i’ qui, tous calculs faits, vaut : i’ = 65,85°. L’inclinaison calculée du rayon sortant avec la verticale du lieu vaut donc : β = 90 – 65,85 = 24,15°.
– d’autre part, l’angle qu’on va appeler γ et qui est celui sous lequel l’observateur situé au sol voit le rayon de l’arc circumzénithal. En pratique, celui-ci se détermine à partir de la 2ème photo présentée [voir annexe]. Tous calculs faits, on trouve : γ = 24,62°.
On constate que l’angle attendu β est pratiquement égal à l’angle mesuré γ.
Ceci signifie que la direction du centre de l’arc circumzénithal vue par l’observateur au sol coïncide avec la verticale du lieu.
Autrement dit, c’est bien un arc circumzénithal qu’Anthony Hémon a photographié !

5) Formation d’un arc coloré avec le violet-bleu au dessus du rouge :
Sur les photos, on constate la formation d’un arc coloré selon les teintes de l’arc-en-ciel distribuées à l’envers, c’est à dire avec le bleu à l’intérieur de la courbure et le rouge à l’extérieur.
Les différentes teintes sont dues au fait que l’indice de réfraction varie avec la longueur d’onde du rayonnement qui traverse le prisme à 90° formé par le cristal de glace.
Comme on l’a vu plus haut, l’indice vu par le rouge est plus faible que celui vu par le bleu ou le violet.

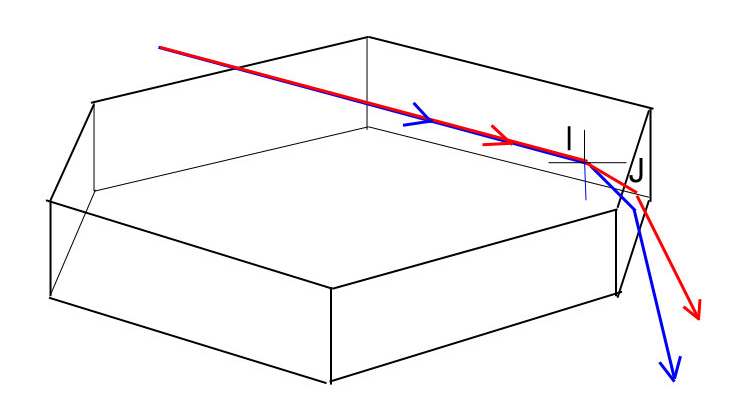Au niveau de la première réflexion en I, la loi de la réfraction de Descartes (sin i = n sin r) permet de de dire que l’angle de réfraction pour le bleu est plus petit que celui pour le rouge.
Au niveau de la 2ème réfraction en J, la situation s’inverse pour l’angle r’ (= 90° – r) qui devient plus grand pour le bleu que pour le rouge.
La loi de Descartes appliquée en ce point (sin i’ = n sin r) nous montre alors que l’angle d’émergence i’ sera plus grand pour le bleu que pour le rouge.
Autrement dit, dans un prisme, le bleu est plus dévié que le rouge…, ainsi que le suggère le tracé des rayons lumineux sur le schéma ci-joint.

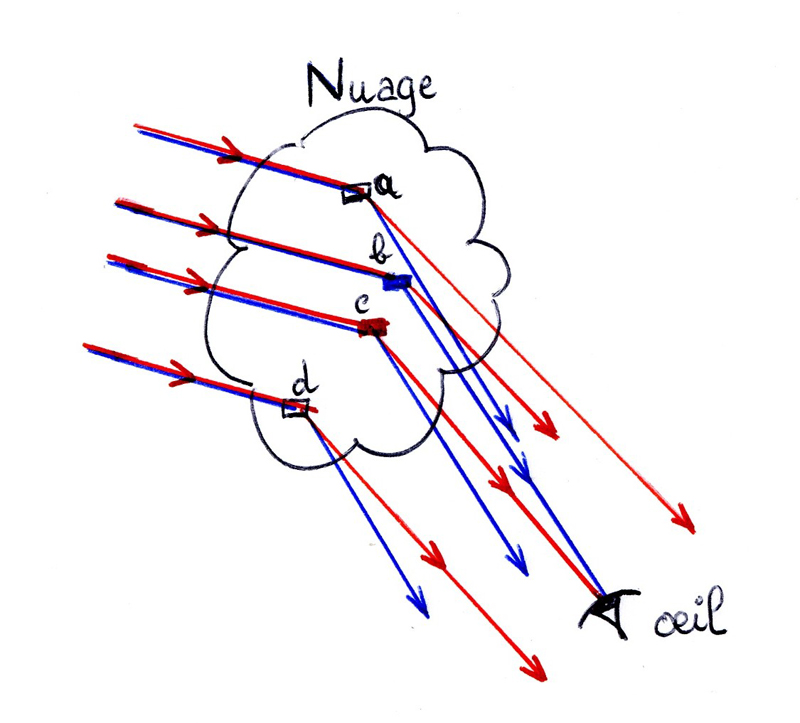Tous les cristaux a, b, c, d contenus dans le nuage (schéma ci-contre) réfractent la lumière, mais l’observateur ne “verra” que ceux : b et c, qui envoient des rayons lumineux en direction de ses yeux. Les cristaux a et d sont ignorés par lui… Il verra donc des cristaux de glace bleus (b) au dessus de cristaux colorés en rouge (c).

6) Conclusion : La fréquence des arcs circumzénithaux est de l’ordre de 13 par an en Europe. Ce n’est donc pas un phénomène très courant. S’il vous intéresse, levez les yeux vers le zénith quand il y a des cirrus dans le ciel. Le matin et le soir, quand le soleil est encore assez bas sur l’horizon, vous aurez peut-être la chance de l’observer. On dit que cet arc est le plus “pur” de tous les phénomènes atmosphériques, alors bonne chasse et bonne chance.

Annexe : calcul de l’angle γ :
On imprime la photo 2 sur une feuille de papier et on détermine de manière géométrique le centre de l’arc en traçant deux cordes et leurs médiatrices : le point de concours est le centre de l’arc. On détermine ensuite la dimension R du rayon sur le capteur. Ceci se fait facilement à partir de la taille du capteur (22,3 X 14,9 mm) dont un des côtés sert d’étalon. On trouve : R = 16,04 mm. Reste à déterminer l’angle γ. Un schéma optique du trajet des rayons lumineux à l’intérieur de l’appareil photo montre que l’angle γ est aussi l’angle sous lequel depuis le centre optique de l’objectif, on voit le rayon R sur le capteur. γ se calcule à partir de sa tangente : tan γ = R/F où F est la distance focale de l’objectif, ici 35 mm. Tous calculs faits, on trouve : γ = 24,62°.

Webographie et bibliographie :
[1] http://opticsaround.blogspot.fr/2012/10/arc-circumzenithal-circumzenithal-arc.html
[2] http://fr.wikipedia.org/wiki/Arc_circumz%C3%A9nithal
[3] Bravais A. Journal de l’Ecole Royale Polytechnique, 18, 1, 1947
[4] D. Lynch, W. Livingston, Aurores, mirages, éclipses, Dunod Editeur, p.159.

Rédaction : Michel Vampouille
Traitement d’image : Denis Lefranc