L’image du mois de juillet 2012 : mesure de la période de rotation du Soleil

Nous allons profiter des belles journées du mois de juillet pour présenter une activité portant sur la mesure de la période de rotation du Soleil. Basée sur l’observation du déplacement des taches solaires, elle peut être réalisée avec un simple appareil photo numérique monté sur un pied classique et équipé d’un zoom optique recouvert d’une feuille de protection qu’on trouve chez tous les revendeurs de matériel astronomique.

ATTENTION : il ne faut jamais regarder directement le Soleil, à l’œil nu, ou avec tout instrument. Utiliser TOUJOURS un filtre atténuateur qui ne laisse passer qu’une très infime partie de l’intensité des rayons solaires.

On présente ici deux images du Soleil prises à deux jours d’intervalle par Michel Vampouille avec un APN EOS 40D équipé d’un téléobjectif de 420 mm recouvert d’une feuille “Astrosolar”. Elles sont issues de deux séries qui ont été réalisées au 1/1000 sec avec une ouverture F/D = 7 à 400 ISO. La première a été faite le 15 juin à 19H 44min 44sec, la seconde le 17 juin à 19H 09min 54sec, ce qui représente un écart temporel de 1,9688 jours entre les images présentées.
Selon les normes relatives à la représentation des photos du Soleil, on a pris soin, après enregistrement des images, de les orienter avec Iris de telle façon que l’axe de rotation Nord-Sud soit vertical. Le protocole expérimental pour obtenir cette disposition sera explicité prochainement dans un article complémentaire.
D’un point de vue technique, chaque photo résulte de l’empilement sous Iris des 5 meilleures images de chaque série (instruction bestof, puis select). Cet empilement, non indispensable mais conseillé, a pour but d’augmenter le contraste des taches.

Sur les deux clichés, on distingue très nettement que la rotation du Soleil a déplacé l’ensemble des taches vers la droite. Un raisonnement trigonométrique simple (s’appuyant sur les trois taches les plus sombres supposées fixées à la surface va nous conduire à une période synodique de rotation de 26.16 jours, résultat en très bon accord avec les valeurs reconnues aujourd’hui .

Si vous voulez suivre les étapes pour réaliser vous-mêmes cette activité, lisez la suite.

Les deux soleils, de même taille, tournés de manière identique avec l’axe de rotation vertical, sont superposés avec un logiciel de traitement d’images (Photoshop ici, mais Picasa ou GIMP sont aussi utilisables).
Cette superposition fait apparaître le mouvement des taches solaires sur des droites perpendiculaires à l’axe de rotation NS. Sur l’image plane représentée ici, la tache A₁ s’est déplacée en A₂, alors que les taches B₁ et D₁ sont passées en B₂ et D₂. En réalité, les points A₁, B₁ et D₁ sont les projections orthogonales sur le segment PQ des taches qui ont tourné autour du point C, sur un cercle horizontal de rayon CQ contenu dans un plan parallèle au plan équatorial.
Pour déterminer l’angle de rotation de chaque tache, il nous faut dessiner ce cercle de rayon CQ, (comme si on l’observait du point N), et repérer sur sa circonférence les positions des taches correspondants aux points A₁ et A₂ que nous noterons : A’₁ et A’₂.

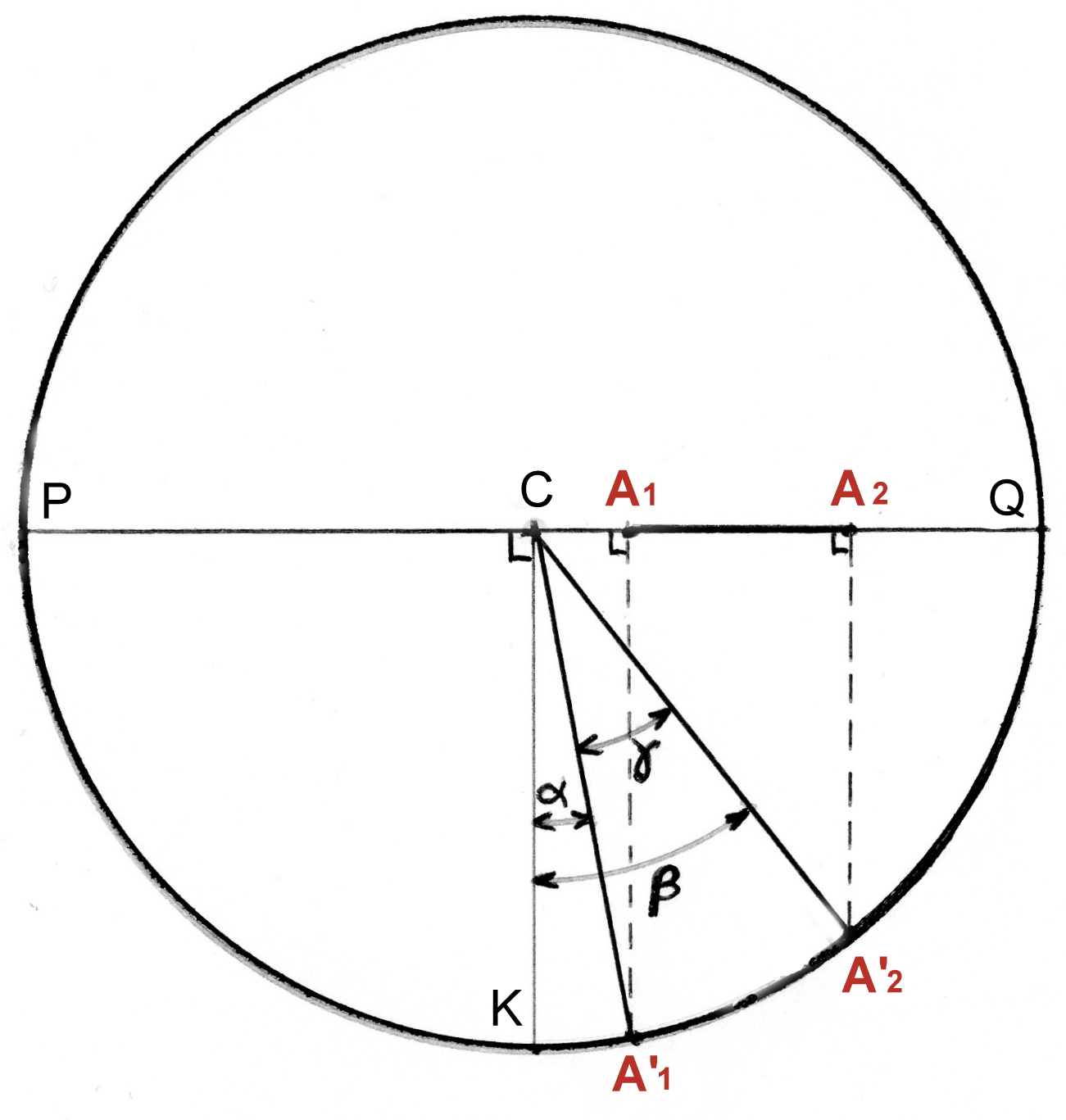Les points A’₁ et A’₂ délimitent un arc de cercle correspondant à la rotation du soleil sur lui-même durant 1,9688 jour. Cet arc de cercle est intercepté par l’angle [A’₁CA’₂], noté γ, qu’il nous faut déterminer à partir des longueurs mesurées sur la photo des soleils superposés.
On a trouvé : CK = CQ = R = 315 pixels ; CA₁ = 20 pixels ; CA₂ = 161 pixels.

Nous allons calculer l’angle g à partir de la relation : γ = β – α, les angles α [= KCA’₁ = CA’₁A₁] et β = [KCA’₂ = CA’₂A₂] étant eux-mêmes calculés à partir de leurs sinus.
sin α = CA₁/R = 20/315 = 0,0635, d’où α = 3,640°.
sin β = CA₂/R = 161/315 = 0,511, d’où β = 30,738°.

L’angle de rotation vaut donc : γ = 30,738 – 3,640 = 27,098°.

Cette rotation s’étant effectuée en1,9688 jour, il est facile de calculer maintenant la période de rotation du Soleil vue depuis la Terre (ou période synodique), notée Tsyn.
Une simple règle de trois (ou un tableau de proportionnalité) nous donne :
Tsyn = (1,9688 x 360)/27,098 = 26,16 jours au niveau de la latitude du point A₁.

Ce résultat est en très bon accord avec la valeur moyenne habituellement admise de 27 jours terrestres.

Le Soleil n’est pas un objet solide. Il subit une rotation différentielle qui se traduit par des vitesses plus rapides à l’équateur qu’aux pôles.
Pour différentes latitudes, les périodes de rotation sont les suivantes :
– 24 jours à l’équateur, latitude 0°,
– 28 jours à la latitude 30°,
– 30,5 jours à la latitude 60°,
– 31,5 à la latitude 75°.
La latitude du point A1 étant environ de -15°, notre résultat de 26,16 jours est donc pertinent.

Un autre moyen de le prouver consiste à reprendre les calculs détaillés ci-dessus avec les clichés donnés toutes les 90 minutes par la sonde SOHO. L’accord est excellent.

On peut aussi reprendre les calculs avec les autres taches pour mettre en évidence la rotation différentielle.
La tache B₁ (latitude plus basse) donne une période de 26,11 jours sensiblement égale à celle déjà calculée.
La tache D₁ donne une période de 27,36 jours plus longue que la précédente, semblant montrer l’augmentation de la période avec la latitude.

Ces calculs supposent que les taches solaires ne se sont ni déformées, ni déplacées entre les deux instants d’observation.
Pour avoir plus de précision, il faudrait surveiller leur comportement durant le temps de l’expérience.

Note : Cette activité a fait l’objet d’un « TPE » (Travail Personnel Encadré) réalisé avec enthousiasme et brio durant l’année scolaire 2011/2012 par Ophélie, David et Baptiste, 3 élèves de 1^ère du Lycée Gay-Lussac de Limoges, adhérent en qualité de personne morale de la Saplimoges.

Webographie :
http://www.ac-nice.fr/clea/A09.html
http://www.ac-clermont.fr/disciplines/fileadmin/user_upload/SciencesPhysiquesEtChimiques/college/soho.pdf
http://www.fr.wikipedia.org/wiki/Soleil
http://soho.www.­nascom.­nasa.­gov

Rédaction : Michel Vampouille