L’image du mois de janvier 2011 ou comment mesurer des angles avec votre instrument d’observation astronomique

Nous allons commencer l’année 2011 avec l’image bien connue de la lune gibbeuse (auteur : Daniel Debord, 29/01/2007, lunette 800 mm + doubleur, APN Canon EOS 20 D au foyer, 1/125 seconde, 200 ISO) pour essayer de répondre à une question que posent souvent les astrophotographes : comment savoir à l’avance si l’image de tel ou tel objet céleste sera bien enregistrée en entier sur le capteur.

Certains ont recours à des logiciels qui, avec les noms de l’instrument et du capteur, donnent une image de la scène observée. D’autres, à force d’expérience, savent qu’un champ de X degrés est disponible avec leur matériel habituel. Qu’ils viennent à changer quelque chose, et c’est le doute.  Nous allons montrer qu’un petit raisonnement permet aisément de calculer le champ angulaire de tout instrument équipé d’un capteur.  Ou encore de mesurer l’écart angulaire entre deux objets, ou bien le diamètre angulaire d’une planète. Il suffit pour cela de connaître la distance focale de son instrument et les dimensions de son capteur.
Pour illustrer et vérifier notre propos, partons de l’image de la Lune ci-dessus et essayons de retrouver son diamètre angulaire.

Nous allons procéder en deux étapes :
1) la détermination du diamètre de la Lune sur le capteur, connaissant la taille d’un de ses pixels.
2) le calcul de son diamètre angulaire, au moyen d’un petit raisonnement d’optique géométrique et de la notion d’angles en “radians”.

1ère étape : mesure du diamètre de la Lune sur le capteur
Tout d’abord, il convient de connaître la dimension du pixel sur le capteur. En général, cette information est donnée dans la notice, ici : 6,42 µm/pixel. On peut aussi la retrouver avec la taille du capteur et le nombre de pixels. Ici, le capteur mesure 22,5 X 15 mm et compte 3504 X 2336 pixels, ce qui conduit à 6,4212 µm/pixel.
Pour mesurer le diamètre de la Lune (ou un écart angulaire quelconque), il est préférable de travailler sur l’adresse des pixels plutôt que sur les longueurs mesurées à l’écran. On s’affranchit ainsi des éventuelles différences de grandissement horizontal et vertical. Un recadrage peut être effectué, mais il convient de le faire avec un logiciel qui conserve les numéros des pixels. Ici, c’est GIMP, logiciel gratuit, qui a été utilisé pour l’opération de recadrage.

La mesure du diamètre se fait en exportant l’image (recadrée ou non) sur un logiciel qui permet la lecture de l’adresse des pixels pointés avec la souris. IRIS, gratuit lui aussi, convient très bien.

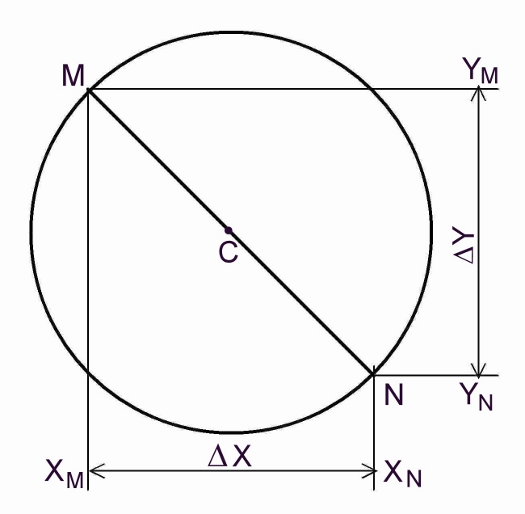
Tout d’abord, il faut repérer avec un maximum de précision sur l’écran, les deux extrémités M et N d’un diamètre qui, en général n’a pas la bonne idée d’être horizontal ou vertical. Ensuite, en pointant la souris sur les points M et N, il faut relever leurs adresses [XM, YM]  et [XN, YN]. Ici, nous avons trouvé :
XM = 1061 ; XN = 2703, d’où on tire  DX = XN – XM = 1642 pixels.
YM = 1989 ; YN = 273, d’où DY = YM – YN = 1716 pixels.
Sachant qu’un pixel mesure 6,4212 µm, on en déduit les longueurs Dx et Dy des composantes horizontale et verticale du diamètre MN.

On trouve : Dx = 1642 x 6,4212 = 10543,6 µm, arrondis à 10,54 mm
Dy = 1716 x 6,4212 = 11018,8 µm arrondis à 11,02 mm.
Le diamètre s’obtient ensuite en appliquant le théorème de Pythagore :
MN = racine carrée [Dx² + Dy²] = 15,25 mm sur le capteur de l’APN (résultat 1).

2ème étape, 1ère partie : modélisation optique du dispositif de mesure
Il nous faut maintenant comprendre comment fonctionne notre dispositif de mesure composé d’un capteur (APN ou caméra CCD) placé dans le plan focal image de l’instrument caractérisé par sa distance focale F. L’instrument pourra être un APN muni de son téléobjectif, une lunette ou bien un télescope.
Pour cela, nous allons le simplifier en disant qu’il est assimilable à une lentille simple convergente de centre optique O, de même distance focale F, placée à la distance F du plan du capteur. Cette simplification, acceptable pour une lunette, un peu moins pour un APN muni d’un téléobjectif, exagérée pour un télescope, donne cependant une description tout à fait exacte du tracé des rayons lumineux au niveau du capteur. Elle est donc compatible avec la mesure que l’on veut effectuer.

Nous nous retrouvons donc avec le schéma optique ci-dessous :

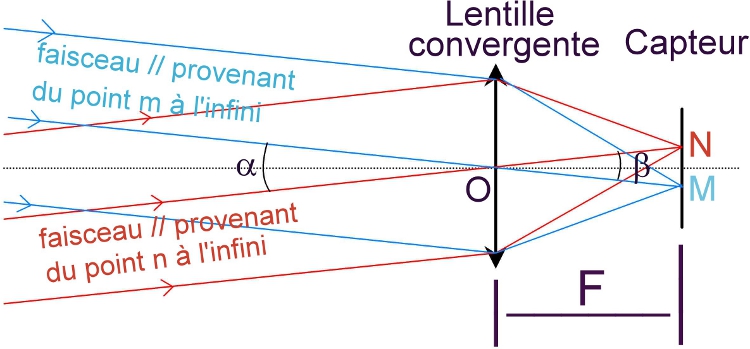
Chacun des points objets m et n situés à l’infini aux extrémités d’un diamètre lunaire mn envoie un faisceau de rayons parallèles qui sont captés par la lentille convergente.
Les directions mO et nO de ces rayons définissent le diamètre angulaire α = mOn que l’on veut mesurer.

Pour continuer, nous allons faire appel à deux propriétés optiques des lentilles simples :
1) Tout rayon incident passant par le centre optique d’une lentille n’est pas dévié → les rayons mO et nO continuent donc selon leurs directions incidentes respectives.
2) Tout faisceau incident de rayons parallèles converge vers un point du plan focal (plan perpendiculaire à l’axe situé à la distance F de la la lentille) qui coïncide avec le plan du capteur quand la mise au point est parfaitement réalisée. En aval de la lentille, les faisceaux vont donc converger vers les points M et N du capteur, ces points étant les “images” des points “objets” m et n.
Les directions OM et ON des rayons émergents définissent l’angle β = MON sous lequel du point O, on voit l’image MN sur le capteur du diamètre de la Lune.
Comme les rayons mO et nO ne sont pas déviés, on voit de suite que : α = β.

Conclusion : l’angle α entre deux objets ponctuels m et n dans le ciel s’obtient donc en mesurant l’angle β sous lequel, du centre optique O de la lentille, on voit leurs images M et N sur le capteur.

2ème étape, 2ème partie : mesure des angles en radians
Pour introduire la notion de radians, partons d’un cercle de rayon R, d’angle au centre 360°, et de sa circonférence C donnée par la relation bien connue : C = 2π.R.
Que représente physiquement le nombre 2π valant : 2 x 3,1416 = 6,2832 ?
On peut dire tout simplement que 2π, c’est le nombre par lequel il faut multiplier le rayon R du cercle pour trouver sa circonférence C.
Si l’on passe au demi-cercle, d’angle au centre 180°, la longueur de son arc circulaire devient C/2 = π.R.
Idem pour le quart de cercle et ainsi de suite… Ainsi, pour un arc de cercle d’angle au centre 30°, ou  360°/12, on trouve sans difficulté que la longueur de l’arc vaut (2π/12).R, soit : π.R/6.
On constate donc qu’il y a une correspondance entre l’angle au centre d’un arc de cercle, mesuré en radian, et la valeur avec laquelle il faut multiplier R pour trouver la longueur de cet arc.
Cette valeur, c’est l’angle en radians au centre de l’arc, et la correspondance s’écrit :
360° ≡ 2π radians (soit : 6,2832 radians), ou bien
180° ≡ π radians (ou : 3,1416 radians)…

On retiendra qu’avec les angles exprimés en radians, la longueur S d’un arc de cercle d’angle α et de rayon R se calcule facilement avec la relation : S = α.R.
De plus, dans le cas des petits angles de quelques degrés qui vont nous intéresser ici (F > 200 mm), on voit qu’on peut assimiler la longueur de l’arc de cercle à celle de la corde qui le sous-tend…!
Prenons comme exemple le calcul de la longueur d’un arc de cercle (ou de sa corde) de rayon 0,5 m et d’angle au centre γ = 1° 45′. Il faut commencer par passer en notation décimale en disant : 1° 45′ = 1° + 45/60 = 1,75°. Puis convertir en radian avec la correspondance donnée plus haut : γ = (1,75 x π)/180 = 0,0305 radian. Et ensuite, calculer la longueur S de l’arc ou de la corde avec S = γ.R = 0,0305 x 0,5 = 0,0152 m = 15,2 mm.

2ème étape, 3ème partie : retour à la mesure du diamètre angulaire de la Lune
Sur le schéma optique ci-dessus, on voit que l’angle β (=α) en radian qui nous intéresse va pouvoir se calculer avec la relation MN = F x β qui se transforme en : β = MN/F.
Ici, nous savons que F = 1600 mm et MN = 15,25 mm (résultat 1).
On en tire β = α = 15,25/1600 = 0,0095 radian.
Il n’y a plus qu’à convertir cette valeur en degrés, minutes et secondes d’arc pour trouver le diamètre angulaire a de la Lune dans les unités habituellement utilisées par les astronomes (minute d’angle notée : ‘, seconde d’angle notée : “, ou millisecondes d’angle notée : msa).
α = (0,0095 x 180)/3,1416 = 0,544° = 0° + (54 x60)/100 = 0° 32,66′ = 0° 32′ + (66 x 60)/100 = 0° 32′ 40″.
D’après nos mesures, le 29 janvier 2007, le diamètre angulaire de la Lune valait : α = 32′ 40″.
Pour cette nuit là, le logiciel Stellarium donne 31′ 42,2″, ce qui conduit à une précision très acceptable de 3,3%.

Nous avons fait confiance aux données du fabricant pour la focale de la lunette (800 mm) et le coefficient du doubleur (X2). L’expérience acquise au fil des ans montre que ces grandeurs doivent être vérifiées avant tout calcul précis. La méthode de mesure des angles présentée ici peut constituer un excellent moyen de vérification. Il suffit de l’appliquer à des étoiles doubles dont on connaît l’écartement angulaire.

Généralisation :
Bien évidemment, le raisonnement est identique quand on remplace les extrémités m et n du diamètre lunaire par deux étoiles. On peut aussi raisonner en sens inverse et se demander quel est le champ angulaire associé à tel ou tel dispositif d’observation. Ainsi avec une lunette de focale F = 500 mm et une CCD rectangulaire de largeur 10,2 mm (Atik 16 HR par exemple), on enregistre un champ angulaire de 10,2/500 = 0,0204 radian ou encore (0,0204 x 180)/3,1416 = 1,17°, soit 1° + (17 x 60)/100 = 1° 10,2′ ou encore 1° 10′ 01″.

Pour toute remarque ou complément d’information sur cet article : contact@saplimoges.fr

Références :
logiciel gimp : http://www.gimp.org/downloads/
logiciel iris : http://www.astrosurf.com/buil/iris/iris.htm
logiciel stellarium : http://www.01net.com/telecharger/windows/Loisirs/astronomie_et_espace/fiches/33514.html

Rédaction : Michel Vampouille