L’image du mois de février 2015 : Cercle parhélique et Paranthélie
Pour le mois de février 2015, voici deux nouveaux phénomènes atmosphériques dus à des cristaux de glace plats hexagonaux illuminés par les rayons solaires. Il s’agit du « cercle parhélique » (à ne pas confondre avec le halo parhélique à 22°) accompagné d’une « paranthélie ».
 Cliquer sur l’image pour l’observer en résolution supérieure.
Cliquer sur l’image pour l’observer en résolution supérieure.
Le « cercle parhélique », c’est une ligne blanche horizontale qui part du Soleil et qui fait un tour complet en restant à la même hauteur angulaire que le Soleil. Ici, c’est l’objectif grand angulaire de l’appareil photographique et la direction inclinée de prise de vue qui transforment la ligne horizontale en une ligne courbe s’élevant aux deux extrémités. Il est constitué de millions de cristaux de glace plats, hexagonaux et orientés qui réfléchissent la lumière du Soleil sur leurs faces verticales. L’éclat du cercle parhélique dépend de l’altitude du Soleil et de l’épaisseur des cristaux.
Quant à la « paranthélie », c’est la tache lumineuse blanche non colorée située ici au centre de l’image et traversée par le cercle parhélique. Cette tache présente la particularité d’être toujours située à 120° du Soleil en azimut. Il peut donc y en avoir deux, une chaque côté du Soleil. Elles résultent des rayons lumineux provenant du Soleil et réfléchis 2 fois sur les faces internes des cristaux de glace hexagonaux.
Ces deux phénomènes atmosphériques sont relativement rares : on en compte une moyenne de 4 chaque année [1-2].
Cette photographie a été prise en Vendée le 11 juin 2011 à 11H14 par David Hémon, fils de Serge, avec un appareil Sony Cyber-Shot.
Parmi les nombreuses formes de glace que peuvent contenir les nuages d’altitude, voir schéma ci-contre [3], ce sont les cristaux hexagonaux « galettes » (notés 1 et 2) qui interviennent dans la formation du cercle parhélique et des paranthélies. Quant aux cristaux « colonnes », ils sont responsables, entre autres, des halos parhéliques et de l’arc circumzénithal qui ont déjà fait l’objet d’articles dans cette rubrique.
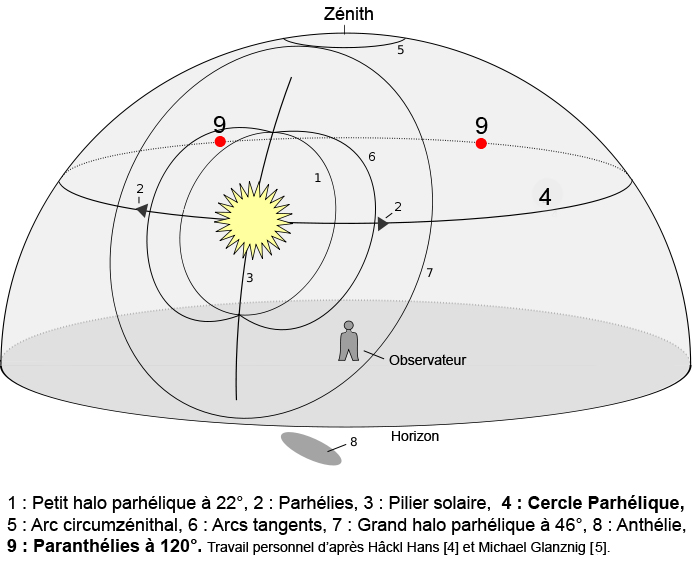
Les phénomènes lumineux présentés appartiennent à la classe des phénomènes peu fréquents (moins de 5 par an). Ces derniers sont recensés sur le schéma de droite.
Quand on observe des parhélies dans le ciel, il faut penser à regarder à 120° de chaque côté du Soleil. Si les conditions météo s’y prêtent, les paranthélies sont visibles.
Formation du Cercle Parhélique
Le Cercle Parhélique résulte de la réflexion des rayons lumineux provenant du Soleil sur une des faces externes verticales des cristaux de glace contenus dans les nuages d’altitude. Dès que l’œil de l’observateur reçoit un rayon réfléchi par un cristal de glace, il voit un point lumineux blanc s’inscrire dans le ciel dans la direction du cristal. S’il y a des millions de cristaux de glace répartis tout autour de l’observateur, la juxtaposition des points lumineux forme une ligne blanche continue faisant un tour complet à la même hauteur que celle du Soleil.
Pourquoi l’observateur voit-il une ligne à la même hauteur que celle du Soleil ?
Pour répondre à cette question, commençons par examiner le trajet d’un rayon lumineux réfléchi au niveau d’un cristal de glace.
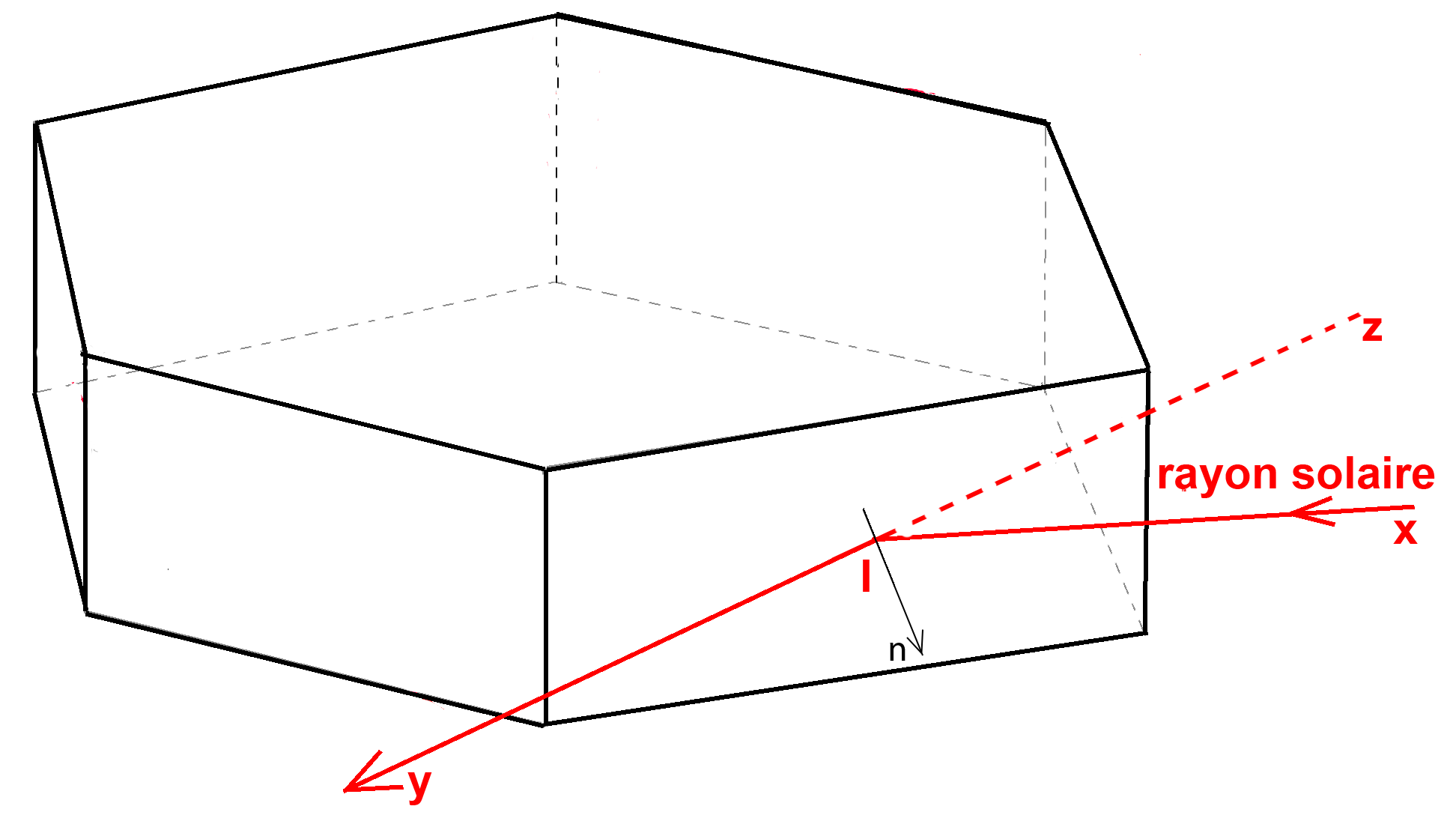 Les grandes faces hexagonales du cristal sont horizontales. Le rayon solaire incident xI tombe en I sur une des faces verticales. La perpendiculaire In à la face et la direction xI du rayon incident définissent un plan particulier qui s’appelle le plan d’incidence. Les lois de Snell-Descartes sur la réflexion nous apprennent que le rayon réfléchi Iy est contenu dans ce plan d’incidence avec l’angle de réflexion yIn égal à l’angle d’incidence nIx. Pour un observateur, ce rayon réfléchi sur ce cristal particulier semblera provenir de la direction yz. Le rayon incident xI et son rayon réfléchi Iy, tous deux contenus dans le plan d’incidence, forment donc le même angle avec un plan horizontal.
Les grandes faces hexagonales du cristal sont horizontales. Le rayon solaire incident xI tombe en I sur une des faces verticales. La perpendiculaire In à la face et la direction xI du rayon incident définissent un plan particulier qui s’appelle le plan d’incidence. Les lois de Snell-Descartes sur la réflexion nous apprennent que le rayon réfléchi Iy est contenu dans ce plan d’incidence avec l’angle de réflexion yIn égal à l’angle d’incidence nIx. Pour un observateur, ce rayon réfléchi sur ce cristal particulier semblera provenir de la direction yz. Le rayon incident xI et son rayon réfléchi Iy, tous deux contenus dans le plan d’incidence, forment donc le même angle avec un plan horizontal.
Conclusion 1 : la direction d’observation yIz donnée par un rayon réfléchi par un cristal frappe le ciel en un point situé à la même hauteur angulaire que le Soleil.
 Examinons maintenant l’influence de tous les cristaux de glace.
Examinons maintenant l’influence de tous les cristaux de glace.
Supposons que le ciel soit rempli de millions de cristaux « galettes » tous horizontaux, mais avec leurs faces latérales orientées de manière quelconque.
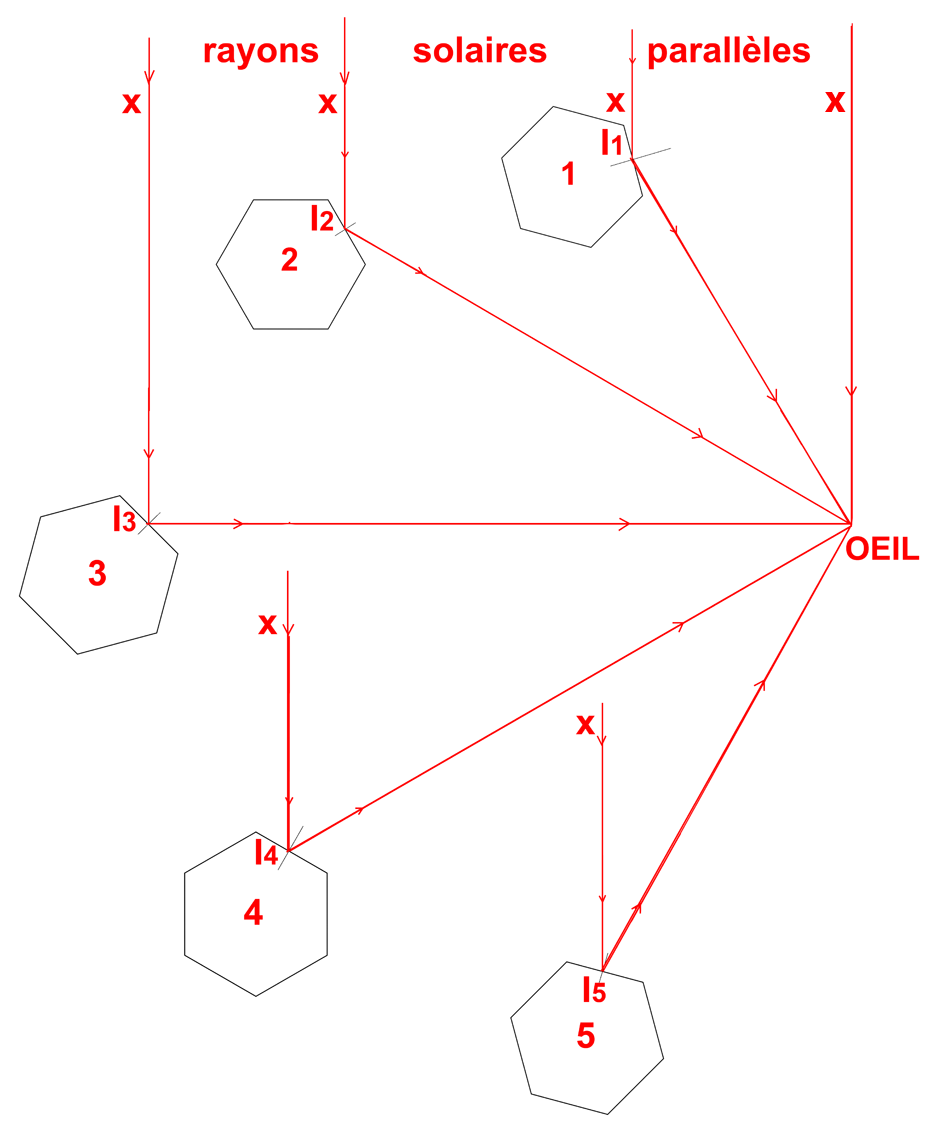
La vue de dessus de cette configuration « naturelle » est représentée sur la figure de droite. Nous n’avons dessiné que 5 cristaux judicieusement placés, mais il faut imaginer qu’il y en partout tournés dans tous les sens.
Les rayons incidents xI1, xI2, xI3, xI4, et xI5 provenant du Soleil sont évidemment tous parallèles. Ils frappent les cristaux sur leurs faces latérales.
Parmi tous les rayons réfléchis dans tous les sens par les différentes faces de tous ces cristaux, il y en a toujours qui arrivent dans l’œil de l’observateur. Ainsi, le cristal 1, dessiné avec une orientation convenable, envoie un rayon réfléchi en I1 vers l’œil. L’œil « voit » alors un point dans le ciel dans la direction œil/I1. De même, le cristal 2, légèrement tourné par rapport au cristal 1, envoie un rayon réfléchi en I2 vers l’œil. L’œil voit alors un nouveau point dans la direction I2. Le même phénomène se reproduit pour les cristaux 3, 4 et 5. L’œil voit des points lumineux dans les directions œil/I3, œil/I4, œil/I5…
Comme les cristaux sont tout petits et qu’ils remplissent tout l’espace, l’ensemble des points lumineux vus par l’observateur forme une ligne horizontale continue dans le ciel dont on a déjà dit plus haut (conclusion 1) qu’elle était à la même hauteur angulaire que le Soleil : c’est le cercle parhélique.
Si les nuages de cristaux sont discontinus, alors le cercle parhélique s’arrête là où il n’y a plus de nuages, comme c’est le cas ici sur la droite de la photo.
Le faible coefficient de réflexion sur chacune des faces de glace, de l’ordre de 1 %, et la petitesse de toutes les surfaces réfléchissantes orientées dans les bonnes directions, expliquent la faible intensité du cercle parhélique.
Formation des Paranthélies à 120°
Les deux paranthélies proviennent de deux réflexions dans le cristal de glace sur deux de ses faces latérales consécutives.
Le schéma ci-dessous illustre le trajet des rayons lumineux conduisant à la paranthélie située à 120° à gauche de la direction du Soleil.
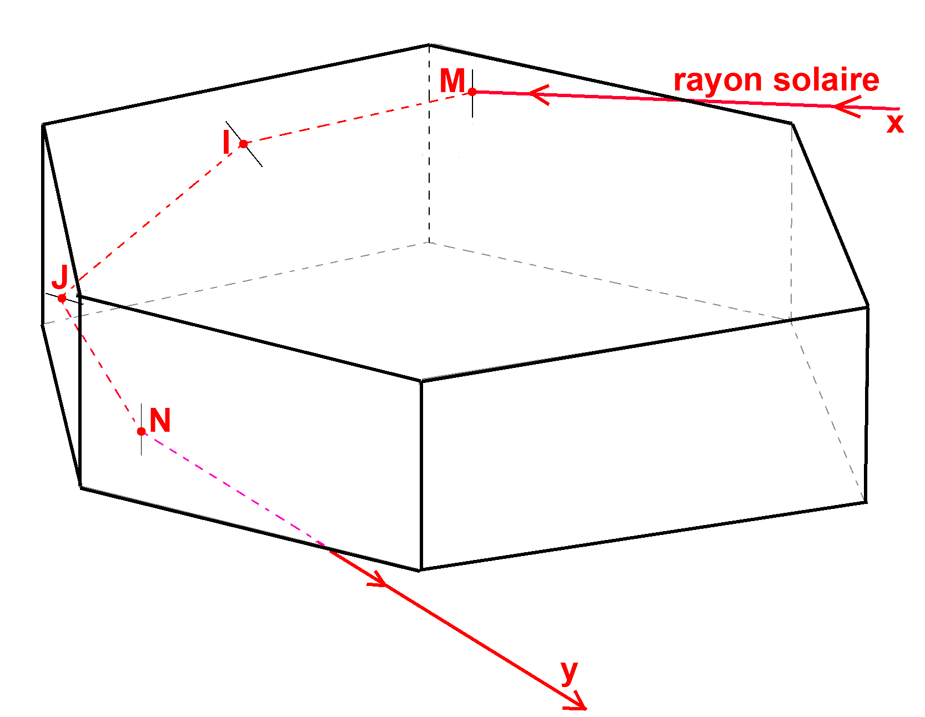 Un des rayons solaires pénètre en M dans le cristal par sa face horizontale supérieure où il est réfracté vers l’intérieur. Ce rayon est ensuite réfléchi une première fois au point I sur une des faces latérales et une deuxième fois au point J, sur la face latérale adjacente. A partir du point J, il est dirigé vers le point N de la face horizontale inférieure sur laquelle il subit une réfraction qui le fait ressortir du cristal. Un observateur placé loin à droite sur le prolongement du rayon Ny verra à la fois, le rayon réfracté provenant du cristal et les rayons solaires directs venant de sa droite.
Un des rayons solaires pénètre en M dans le cristal par sa face horizontale supérieure où il est réfracté vers l’intérieur. Ce rayon est ensuite réfléchi une première fois au point I sur une des faces latérales et une deuxième fois au point J, sur la face latérale adjacente. A partir du point J, il est dirigé vers le point N de la face horizontale inférieure sur laquelle il subit une réfraction qui le fait ressortir du cristal. Un observateur placé loin à droite sur le prolongement du rayon Ny verra à la fois, le rayon réfracté provenant du cristal et les rayons solaires directs venant de sa droite.
Il nous faut maintenant expliquer 2 points :
- Pourquoi le rayon sortant Ny pointe-t-il dans le ciel vers un point situé à la même hauteur angulaire que le Soleil ? Autrement dit, pourquoi la paranthélie est-elle située sur le cercle parhélique ?
- Pourquoi le rayon sortant est-il toujours orienté à 120° en azimut par rapport à la direction du Soleil ?
Pour répondre à la question 1, il faut revenir à la conclusion 1 donnée plus haut : les 3 rayons internes MI, IJ et JN appartiennent tous au même plan d’incidence défini par MI et la perpendiculaire en I à la face latérale verticale sur laquelle MI va se réfléchir. Autrement dit, la hauteur angulaire de ces 3 rayons par rapport à l’horizontale est la même. On peut donc affirmer que s’il n’y avait pas eu de réflexions aux points I et J (par exemple, avec une galette de grande surface), le rayon MN serait rectiligne. On se retrouve alors dans le cas classique du passage d’un rayon lumineux à travers une lame de glace à faces parallèles dont le schéma est représenté ci-dessous.
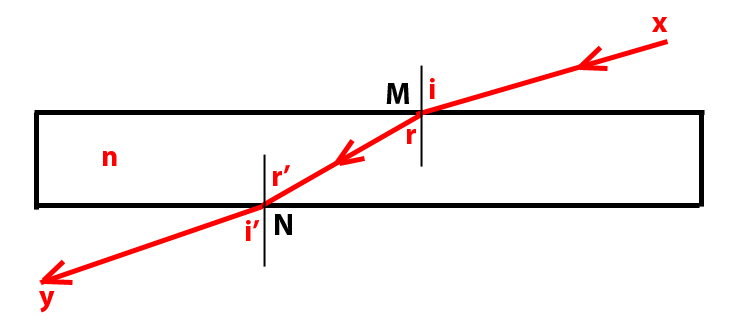 Un rayon solaire xM frappe la face horizontale supérieure du cristal en faisant un angle d’incidence i avec la perpendiculaire en M à la face. Il est réfracté dans le plan d’incidence (celui de la page) selon la direction MN en faisant un angle de réfraction r conformément à la loi de Snell-Descartes :
Un rayon solaire xM frappe la face horizontale supérieure du cristal en faisant un angle d’incidence i avec la perpendiculaire en M à la face. Il est réfracté dans le plan d’incidence (celui de la page) selon la direction MN en faisant un angle de réfraction r conformément à la loi de Snell-Descartes :
sin i = n sin r, où n est l’indice de réfraction de la glace.
Ce rayon intérieur est ensuite réfracté en N par la face horizontale inférieure selon la loi :
n sin r’ = sin i’, avec r’ : angle d’incidence sur la face et i’ : angle de réfraction (ou d’émergence).
Finalement, le rayon lumineux ressort du cristal de glace selon la direction Ny.
Il est évident que les angles r et r’ sont égaux. On en déduit de suite que l’angle d’incidence i est égal à l’angle d’émergence i’. Par conséquent, les rayons incident xM et émergent Ny sont parallèles. Autrement dit, un observateur qui reçoit le rayon émergent Ny verra le Soleil à la même hauteur angulaire que s’il n’y avait pas de cristal de glace.
Ceci est aussi vrai sur le schéma de départ pour le trajet réel du rayon lumineux ayant subi deux réflexions internes dans le cristal.
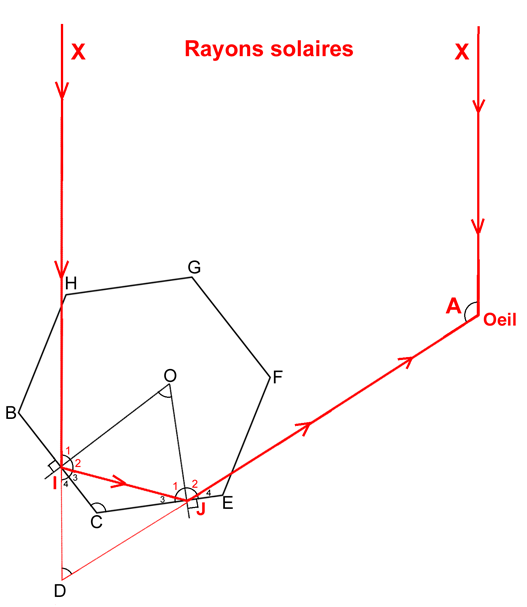 Pour répondre à la question 2, il nous faut un nouveau schéma représentant un cristal de glace vu de dessus.
Pour répondre à la question 2, il nous faut un nouveau schéma représentant un cristal de glace vu de dessus.
L’œil de l’observateur regarde à la fois les rayons solaires x/Œil provenant du Soleil, et ceux J/Œil résultant d’une double réflexion interne dans le cristal de glace. Compte-tenu des démonstrations précédentes, nous n’avons pas fait figurer les points M et N d’entrée et de sortie sur les faces horizontales qui n’ont aucun effet sur les directions des rayons lumineux quand on les regarde de dessus. Ce qu’il nous faut expliquer c’est pourquoi l’angle A entre les rayons directs et les rayons en provenance du cristal vaut toujours 120° et ceci quelle que soit son orientation.
On remarque :
– Angle réfléchi I2 = angle incident I1. L’angle I3, ayant pour complément I2, est égal à l’angle I4, car celui-ci a pour complément I1, égal à I2.
– De même : J1 = J2 et J3 = J4.
– Dans le triangle IDJ, l’angle D vaut 180° – (I3 + I4 + J3 =J4), ou encore, d’après les remarques ci-dessus, D = 180° – 2(I3 + J3).
– Dans le triangle CIJ, la somme des angles (I3 + J3) = 180° – C, avec C = 120°, car angle entre 2 côtés adjacents d’un hexagone.
– Il vient donc : (I3 + J3) = 180° – 120 = 60°.
– En reportant ce résultat dans la ligne du dessus, on obtient : D = 180° – 2×60° = 60°.
– Et enfin, le résultat cherché : A = 180° – D = 180° – 60° = 120°, quel que soit l’angle d’incidence I1.
Conclusion : dans une direction à 120° des rayons solaires directs, l’observateur voit une tache blanche fixe qu’on appelle une paranthélie. En présence de nuages renfermant des cristaux de glace de forme « galette », une tache symétrique existe aussi de l’autre côté.
Retour sur le cercle parhélique : en toute rigueur, il faut noter que les rayons réfléchis une seule fois sur une face interne contribuent aussi à la formation du cercle parhélique. Dans cette configuration, les rayons solaires pénètrent dans le cristal par la face horizontale supérieure où ils sont réfractés. Ils sont ensuite réfléchis par une seule des faces latérales internes, et ressortent après une nouvelle réfraction par la face horizontale inférieure. Contrairement aux deux paranthélies, les directions des rayons émergents sont quelconques, car cette fois, elles dépendent de l’angle d’incidence I1 et de l’orientation de la face réfléchissante.
Bonne chasse aux phénomènes atmosphériques « rares »…
Note du photographe : la petite trace blanche qu’on voit à gauche, au dessus de la paranthélie est celle d’un avion Airbus 380.
Bibliographie et Webographie :
[1] http://fr.wikipedia.org/wiki/Cercle_parh%C3%A9lique
[2] http://la.climatologie.free.fr/pheno-optique/optique2.htm#4
[3] http://www.atoptics.co.uk/halo/platcol.htm
[4] .
[5] http://fr.wikipedia.org/wiki/Parh%C3%A9lie#mediaviewer/File:Halo_overview.svg
Rédaction : Michel Vampouille.


Laisser un commentaire