Pour l’image du mois d’août 2013, nous proposons une image classique mais toujours spectaculaire, réalisable sans matériel sophistiqué par tout amateur soigneux et méthodique : une rotation d’étoiles autour de la Polaire sur un fond de ciel bleu contrastant avec un premier plan composé ici d’une viorne en fleurs (viburnum caprifoliacaea). Ce cliché a été obtenu en juin 2013 à Limoges par José Fernandez en cumulant sans aucun réalignement un ensemble de 131 poses consécutives séparées de 30 secondes. Cliquer dessus pour l’obtenir en résolution supérieure.
Les différentes poses ont été enregistrées dans la nuit du 7 au 8 juin 2013 avec un APN Canon EOS 600 D équipé d’un objectif Canon 50 mm, réglé à F/2.8, 800 ISO, et monté sur un pied photo classique sans motorisation. C’est le mouvement de rotation de la Terre autour de l’étoile polaire qui fait apparaître les traînées d’étoiles en arcs de cercle.

Nous avons déjà publié en mai 2010 une image similaire. Réalisée par Christophe Mercier, elle nous a permis d’évaluer la durée du jour sidéral. Mais la précision obtenue était insuffisante pour conclure. La photo et le calcul correspondants ont cependant été repris par la revue Astronomie Magazine pour un article qui a été publié dans le numéro du mois de juillet/août 2012 [1].
Sur la photo présentée ici, José a choisi de porter à plus d’une heure le temps de pose global, d’ajouter un premier plan et de préserver la couleur bleue du ciel. Cet ajout d’esthétisme ne gênera nullement pour le calcul de la durée du jour sidéral dont la précision devrait être améliorée par le doublement du temps de pose.

Modalités de prise de vue :
Les enregistrements ont été programmés au moyen d’un intervallomètre classique : 131 poses de 10 secondes chacune, séparées de 30 secondes. Le temps de pose unitaire de 10 secondes a été choisi pour obtenir un fond de ciel bleu en harmonie avec les couleurs verte et blanche du premier plan.
Le décompte du temps de pose global après empilement des 131 photos, noté T, se fait facilement avec le petit calcul suivant : T = 130 images X 30 secondes + 10 secondes pour la 131^ème = 65 minutes 10 secondes ou 65,17 minutes en notation décimale.
A noter que le codage Exif aboutit au même résultat :
photo n°1 :7 juin,23H 16min 58.39sec,photo n° 131 : 8 juin, 00H 21min 59.00sec,
ce qui donne 65min 0,21 sec auxquelles il faut ajouter les 10 secondes d’exposition de la 131^ème photo, pour la durée globale T de chaque arc de cercle sur la photo présentée, soit 65min 10,21sec.

Technique d’empilement :
Les 131 photos sont ensuite empilées les unes sur les autres au moyen du logiciel gratuit Starstax [2,3]. Ce logiciel, tout comme Starmax {4], a été spécialement développé pour créer des photos composées montrant le mouvement des astres dans le ciel. Très facile d’emploi une fois que les photos sont sauvegardées, il n’additionne en fait que le déplacement des étoiles. Le fond de ciel et le premier plan restent ainsi exposés correctement.
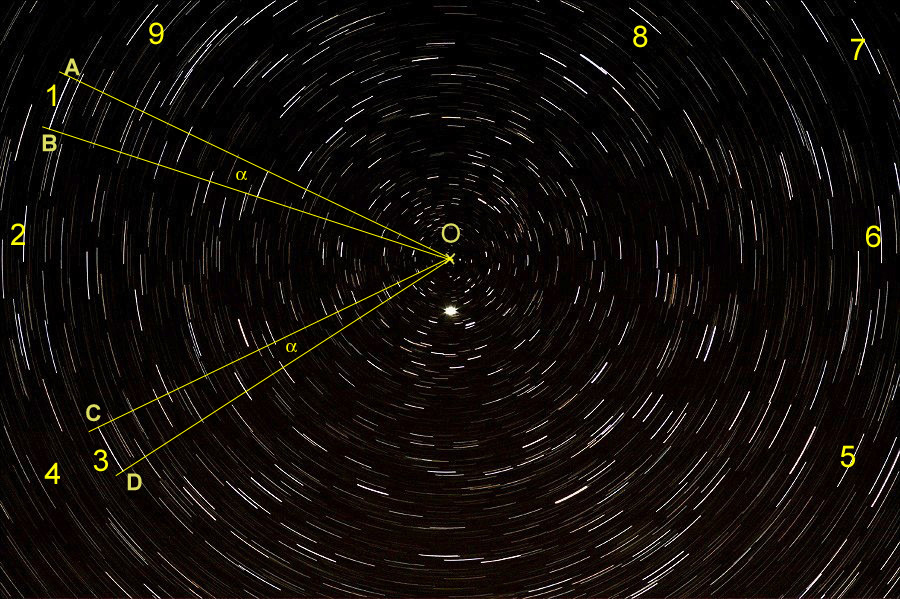
L’empilement terminé, on obtient un filé d’étoiles sur le tableau composant la 1^ère image. Ce résultat peut être éventuellement retouché avec n’importe quel logiciel de traitement d’images. Sur la photo ci-dessous, nous avons dessiné avec Photoshop les éléments utiles pour les mesures ultérieures.

Évaluation de la durée d’un jour sidéral :
Le jour sidéral correspond à une rotation de la Terre de 360° autour de son axe, ou bien à une rotation d’un tour complet par rapport aux étoiles autres que notre Soleil. Il est différent du jour solaire qui se mesure entre les deux instants consécutifs où le soleil se retrouve à la verticale d’un même lieu. Pendant que la Terre fait un tour complet sur son axe, elle progresse sur son orbite autour du Soleil. Ele doit donc tourner encore un peu pour retrouver le Soleil à la verticale du lieu considéré.
La durée du jour sidéral est invariable : 23h 56min 04,1sec.
Celle du jour solaire varie, jusqu’à + ou – 14 minutes, en fonction de la position de la Terre sur son orbite autour du Soleil, et plus précisément en fonction de sa vitesse (variable) sur sa trajectoire elliptique. Sa durée moyenne sur une période d’un an est de 24h 00min 00sec. C’est la durée ″officielle″ du jour solaire. Elle est supérieure à celle du jour sidéral.

Pour évaluer la durée du jour sidéral, on procède selon les trois étapes déjà décrites dans l’article de mai 2010 :

1°) Après avoir repéré et numéroté les arcs de cercle les plus contrastés sur une image agrandie au maximum et imprimée sur un calque transparent, on détermine leur centre commun, noté O, qui est le point de concours des médiatrices des cordes AB, CD, EF, …..

2°) On détermine ensuite les angles au centre, nommés α_i, interceptant les 6 arcs de cercle repérés. Pour cela, on mesure le plus précisément possible la longueur de chaque corde : AB, BC, DE, ….., et de chaque rayon : OA, OC, OE, …. Le lien entre l’angle α, la corde AB et son rayon est donné par : sin (α/2) = AB/2.OA.
Avec une calculette, il est alors facile de calculer l’angle α_i pour chaque arc de cercle. On obtient le tableau suivant :

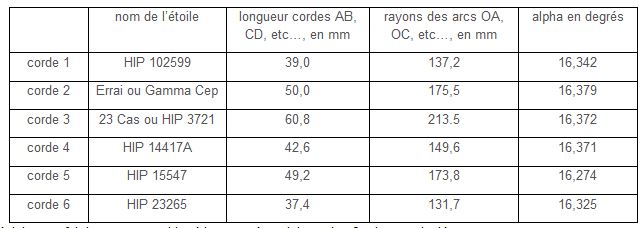Pour augmenter la précision, on fait la moyenne arithmétique, notée <α>, des 6 valeurs calculées.
Tous calculs faits, on trouve : <α> = 16,344°.
Ceci signifie que pendant une durée de 65,17 minutes, la Terre a tourné sur elle-même de cet angle.

3°) On détermine enfin la durée du jour sidéral, noté Tjs :
Sachant qu’un tour complet de la Terre correspond à 360°, il est facile de calculer Tjs en minutes avec la relation :
Tjs = 360.T/<α> = 360×65,17/16,344 = 1435,47minutes,

soit : Tjs = 23h 55min 28sec, valeur très proche des 23h 56min 4,1sec escomptées.

4°) On s’intéresse à la précision de la mesure :
La précision sur le résultat provient essentiellement de la mesure des cordes sur l’agrandissement. On peut estimer que les segments AB, CD, EF, etc… sont mesurés sur l’image agrandie avec une erreur absolue de 0,2mm, alors que les segments font 47mm en moyenne. Ceci nous conduit à une précision (ou erreur relative) de 0,2/47 = 0,4% sur chaque valeur de α. Ensuite, on peut estimer que la moyenne arithmétique sur 6 mesures divise cette erreur d’un facteur 2.
La précision sur la valeur de <α> tombe donc à 0,2% environ.
Celle-ci se retrouve identique sur la valeur de Tjs.
L’erreur absolue sur Tjs vaut alors : Tjsx0,2%, soit 3 minutes environ.

Notre résultat final s’écrit donc : Tjs = 23h 55 min ± 3 min.

A noter, que comme attendu, la valeur trouvée ici est plus proche de la valeur réelle que celle de 2010 (23h 58 min 4 sec ± 10 min) et que la précision est supérieure (3 min au lieu de 10). Pour faire mieux, il faudrait encore augmenter le temps de pose global… !
A vous de jouer ! Avec une belle composition en premier plan, l’aventure est au bout de la nuit !

Pour tout commentaire ou information sur cet article : contact@saplimoges.fr.

Webographie :

[1] Astronomie Magazine N°147, juillet/août 2012.
[2] http://starstax.fr.malavida.com/
[3] http://makipix.com/timelapse-et-trainees-detoiles-autour-de-polaris/
[4] http://www.photopassion.fr/tuto-photo-le-file-detoiles-avec-starmax-23

Rédaction : Michel Vampouille

Pour l’image du mois de mai, nous restons dans le domaine des filés avec cette rotation classique d’étoiles autour de la polaire. Pourquoi une telle image ?
Tout d’abord, parce qu’elle est accessible à tout amateur qui possède un APN avec pose B et un simple pied photographique classique sans motorisation.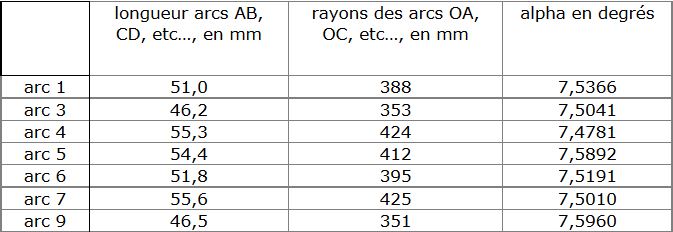
Ensuite parce qu’elle permet de faire des compositions bien sympathiques avec des premiers plans savamment sélectionnés : on en trouve une grande quantité sur Internet, toutes plus jolies les unes que les autres [1].
Enfin, et ce sera notre propos, elle va nous servir de référence pour tenter de calculer le temps que met la Terre pour faire un tour complet de 360° autour de son axe de rotation, c’est-à-dire la durée d’un jour sidéral [2] qui est de 23heures 56minutes 4,09 secondes.

Aura-t-on assez de précision avec le cliché présenté pour affirmer que la durée d’un jour sidéral est différente de celle d’un jour solaire ?
Le temps de pose étant insuffisant, la réponse est négative.
Mais alors, combien de temps doit-on poser pour espérer trouver un résultat avec une erreur absolue de 1 ou 2 minutes ?
Si vous êtes impatient de connaître le résultat, sachez qu’il faut prévoir un temps de pose d’environ 3 heures ! Si le raisonnement vous intéresse, lisez la suite…

La photographie ci-dessus a été obtenue en mai 2009 par Christophe Mercier à Azerables (23160) avec un APN Canon EOS 40 D équipé d’un objectif Sigma de focale 105 mm ouvert à F/5,6, réglé sur 400 ISO, pointé avec un pied Manfrotto sans motorisation dans la direction de l’étoile polaire. Le temps de pose global est de 30 minutes 5 secondes, correspondant à l’empilement sous IRIS (Starmax convient aussi très bien) de 6 poses de 5 minutes séparées de 1 seconde. En procédant ainsi, on obtient un fond de ciel relativement noir sur lequel les trajectoires circulaires des étoiles se détachent bien.

Pour calculer la durée notée Tjs d’un jour sidéral, nous procédons en 3 étapes :

1) On commence par déterminer le centre de rotation, noté O, de toutes les trajectoires des étoiles. Ceci se fait sur un calque posé sur un agrandissement papier de l’image présentée. Le centre de rotation O est le point de concours des médiatrices [3] tracées avec soin au compas de plusieurs trajectoires circulaires des étoiles les plus éloignées (numérotées pour faciliter leur repérage). On constate, comme prévu, que le point O, replacé sur la photo, ne coïncide pas avec l’étoile polaire (étoile surexposée au centre). Il en est distant actuellement de 40 minutes d’angle environ.

Ensuite, on mesure l’angle au centre, noté α
Cet angle intercepte les arcs de cercle numérotés correspondant à la rotation de la Terre pendant une durée T de 30 min 5 sec (ou 30,083 minutes en notation décimale).
Pour obtenir un maximum de précision, on peut travailler sur une impression d’écran de la partie considérée agrandie au maximum. Un rapporteur d’angles donne une faible précision. Une autre méthode plus précise consiste à mesurer avec soin la longueur des arcs de cercle AB, CD, etc….., et d’en déduire les angles α correspondants par le calcul des sinus des angles moitié avec la relation :
sin (α/2) = AB/2OA [4].
Avec la relation ci-dessus et un agrandissement maximum sur l’écran, nous avons obtenu le tableau de mesures suivant :
En faisant la moyenne arithmétique des valeurs obtenues, on trouve : α = 7,5320°. Ceci signifie que pendant une durée de 30,083 minutes, la Terre a tourné de cet angle sur elle-même.

3) On calcule enfin la durée Tjs d’un jour sidéral : sachant qu’un tour complet correspond à 360°, il est facile de calculer Tjs en minutes avec la relation :
Tjs = 360.T/α = 360×30,083/7,532 = 1437,85 minutes, ou encore : Tjs = 23h 57min 51sec, ce qui est très proche des 23h 56min 4sec escomptées…

4) Quelle est la précision sur cette mesure ?
L’imprécision sur le résultat provient de la mesure des arcs de cercle et de leurs rayons. On peut estimer que les segments AB, CD, etc… sont mesurés sur l’image agrandie avec une erreur absolue de ±0,3mm, alors que les segments font 50 mm en moyenne. Celle des rayons OA, OC, etc… est évaluée à  ±1mm sur 400 en moyenne. Ceci nous conduit à une précision (ou erreur relative) de 0,3/50 + 1/400 ≈ 0,8% sur la valeur de α. Celle-ci se retrouve identique sur la valeur de Tjs. L’erreur absolue est donc égale à 0,8.Tjs/100, soit 12 minutes environ. Notre résultat s’écrit donc :

Tjs = 23h 58 min ± 12min, ce qui ne permet pas de différentier la durée d’un jour sidéral de celle d’un jour solaire.

Pour descendre l’erreur à 2 minutes toutes choses égales par ailleurs, il faut la diviser par 6, ce qui revient grosso-modo à multiplier par 6 la longueur des arcs de cercle et donc à prendre un temps de pose 6 fois plus long. Ceci signifie que dans les conditions de notre expérience, il faut poser durant 3 heures au minimum si on veut affirmer, preuve à l’appui, que la différence de durée entre un jour solaire et un jour stellaire est supérieure à 2 minutes. Ceci est à la portée d’un amateur motivé un peu aguerri, mais nous ne l’avons pas encore fait !!!

Pour tout commentaire ou information sur cet article : contact@saplimoges.fr

Références :
[1] http://images.google.fr/images?…..8&source=og&sa=N&hl=fr&tab=wi
[2] http://fr.wikipedia.org/wiki/Jour_sid%C3%A9ral
[3] http://www.mathsgeo.net/rep/dmed.html
[4] http://mathocollege.free.fr/brevet/angles/angles.html

Rédaction : Michel Vampouille